Abstract
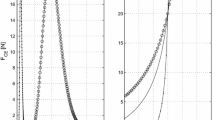
We developed muscle–tendon models incorporating Hill-type structure and length-dependent coupling between activation and velocity. The models were evaluated in electrically stimulated cat soleus muscles. Dynamic model parameters were estimated by a nonlinear parameter estimation algorithm from input–output data obtained during simultaneous random stimulation and length changes. Static parameters were estimated from the length–tension curve. A model with length history-dependent activation–velocity coupling predicted the behavior of the muscle under a wide variety of conditions, including during random perturbations and during isovelocity movements, where it captured short range stiffness and length history-dependent postyielding behavior. Furthermore, the model predicted twitch responses. The generality of this fixed parameter model makes it especially suitable for simulation and feedforward control, where muscle responses are not available for on-line parameter adaptation.
Similar content being viewed by others
REFERENCES
Bernotas, L. A., P. E. Crago, and H. J. Chizeck. A discretetime model of electrically stimulated muscle. IEEE Trans. Biomed. Eng.33:829-838, 1986.
Chizeck, H. J., N. Lan, L. Streeter-Palmieri, and P. E. Crago. Feedback control of electrically stimulated muscle using simultaneous pulse width and stimulus period modulation. IEEE Trans. Biomed. Eng.38:1213-1224, 1991.
Crago, P. E. Muscle input-output model: The static dependence of force on length, recruitment and firing period. IEEE Trans. Biomed. Eng.39:871-874, 1992.
Crago, P. E., M. A. Lemay, and L. Liu. External control of limb movements involving environmental interactions. In: Multiple Muscle Systems. Biomechanics and Movement Organization, edited by J. M. Winters and S. L-Y. Woo. New York: Springer, 1990, pp. 343-359.
Crago, P. E., N. Lan, P. H. Veltink, J. J. Abbas, and C. Kantor. New feedback control strategies for neuroprosthetic systems. J. Rehab. Res. Dev.33(2):158-172, 1996.
Dennis, J. E., Jr., D. M. Gay, and R. E. Welsch. NL2SOL: An Adaptive Nonlinear Least-Squares Algorithm. ACM Trans. Math. Software7(3):369-383, 1981.
Durfee, W. K., and K. E. MacLean. Methods for estimating isometric recruitment curves of electrically stimulated muscle. IEEE Trans. Biomed. Eng.36:654-667, 1989.
Hindmarsh, A. C. Odepack: a systematized collection of ode solvers. In: Scientific Computing, edited by R. S. Stepleman et al.Amsterdam: North-Holland, 1983, pp. 55-64.
Huxley, A. F. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem.7:257-318, 1957.
Joyce, G. C., P. M. H. Rack, and D. R. Westbury. The mechanical properties of cat soleus muscle during controlled lengthening and shortening movements. J. Physiol. (London)204:461-474, 1969.
Kirsch, R. F., D. Boskov, and W. Z. Rymer. Muscle stiffness during transient and continuous movements of cat muscle: Perturbation characteristics and physiological relevance. IEEE Trans. Biomed. Eng.41:758-770, 1994.
Rack, P. M. H., and D. R. Westbury. The effects of length and stimulus rate on tension in the isometric cat soleus muscle. J. Physiol. (London)204:443-460, 1969.
Rack, P. M. H., and D. R. Westbury. The short range stiffness of active mammalian muscle and its effect on mechanical properties. J. Physiol. (London)240:331-350, 1974.
Rack, P. M. H., and D. R. Westbury. Elastic properties of the cat soleus tendon and their functional importance. J. Physiol. (London)347:479-495, 1984.
Scott, S. H., and G. E. Loeb. The mechanical properties of the aponeurosis and tendon of the cat soleus muscle during whole-muscle isometric contractions. J. Morphol.224(1):73-86, 1995.
Shue, G., P. E. Crago, and H. J. Chizeck. Muscle-joint models incorporating activation dynamics, moment-angle, and moment-velocity properties. IEEE Trans. Biomed. Eng.42:212-223, 1995.
Talbot, J. A., and D. L. Morgan. Quantitative analysis of sarcomere non-uniformities in active muscle following a stretch. J. Muscle Res. Cell Motil.17(2):261-268, 1996.
Winters, J. M. Hill-based muscle models: A systems engineering perspective. In: Multiple Muscle Systems. Biomechanics and Movement Organization, edited by J. M. Winters and S. L-Y. Woo. New York: Springer, 1990, pp. 94-100.
Yamaguchi, G., and F. E. Zajac. Restoring unassisted natural gait to paraplegics via functional neuromuscular stimulation: A computer simulation study. IEEE Trans. Biomed. Eng.37:886-901, 1990.
Zahalak, G. I. A distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci.55:89-114, 1981.
Zahalak, G. I. A comparison of the mechanical behavior of the cat soleus muscle with a Distribution-Moment model. J. Biomech. Eng.108:131-140, 1986.
Zahalak, G. I. An overview of muscle modeling. In: Neural Prostheses. Replacing Motor Function After Disease of Disability, edited by R. B. Stein, P. H. Peckham, and D. P. Popovic. New York: Oxford University Press, 1992, pp. 17- 57.
Zajac, F. E. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. CRC Crit. Rev. Biomed. Eng.17:359-411, 1989.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Shue, Gh., Crago, P.E. Muscle–Tendon Model with Length History-Dependent Activation–Velocity Coupling. Annals of Biomedical Engineering 26, 369–380 (1998). https://doi.org/10.1114/1.93
Issue Date:
DOI: https://doi.org/10.1114/1.93