Wavelet-Based Multifractal Analysis of Human Balance

Abstract

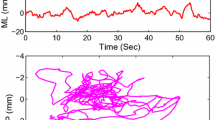
Center of pressure (COP) traces have been used to investigate the dynamics of human balance. In this paper we employ a wavelet-based multifractal methodology to identify structural differences in mediolateral and anterioposterior sway between COP traces of healthy and Parkinson's patients. Two statistical techniques are used to summarize the differences in multifractal spectrum (MFS) for both groups. The first technique is a multivariate repeated measures analysis on estimated MF spectra for subjects. The second technique obtains two characteristic measures from each subject's estimated MFS: (i) location and (ii) half-width of the spectrum. These measures present an intuitive summary of the MFS for each subject, allowing for statistical comparisons between the two groups. Both analyzes lead to significant discrimination between Parkinson versus healthy subject's MFS. We find that COP time series of Parkinson patients exhibit a greater degree of roughness as compared to healthy subjects' COP traces. Furthermore, MFS for Parkinson patients are narrower, suggesting a reduction in complexity as compared to the healthy group. The methodology presented here may be helpful in development of clinically relevant measures, including the assessment of severity of conditions as the measures developed here correlate with standard severity measures. © 2002 Biomedical Engineering Society.

PAC2002: 8719Bb, 8719St, 0250Sk, 8719Xx, 0545Df, 0230Uu