Tumour control probability derived from dose distribution in homogeneous and heterogeneous models: assuming similar pharmacokinetics, ¹²⁵Sn–¹⁷⁷Lu is superior to ⁹⁰Y–¹⁷⁷Lu in peptide receptor radiotherapy

Peptide receptor radiotherapy is commonly used in the second or the third line for metastatic neuroendocrine tumours, where each patient usually displays a wide panel of tumour geometries ranging from large heterogeneous tumours down to undetectable millimetric tumours. Patient outcome is intimately linked to the least controlled tumour geometry. It was already shown by O'Donoghue et al (1995) and is commonly known since the introduction of dosimetry software, such as MIRDOSE 3.0 (Stabin 1996), the precursor of OLINDA/EXM (Stabin et al 2005) , that beta emitters with a large range, such as ⁹⁰Y (12 mm maximal range) are not suitable to cure millimetric tumours. ¹⁷⁷Lu, with its shorter beta maximal range (1.5 mm) was already tested by Rames (1959). More recently, in view of its good chelating stability, it was proposed as a better alternative to ⁹⁰Y for peptide receptor radiotherapy (Kwekkeboom et al 2001) and is now commonly used.

However, when introducing ¹⁷⁷Lu, concerns soon appeared about the efficacy of ¹⁷⁷Lu to cure heterogeneous tumour where the centre of regions without uptake could not be reached by the beta emitted from the surrounding taking up tissue. Intuitively, it was already admitted that a combination of ⁹⁰Y–¹⁷⁷Lu should be better suited to simultaneously treat small homogeneous tumours and large heterogeneous tumours. The pioneer work of de Jong et al (2005) on a rodent tumour model proved the validity of this concept.

Clinical trials using a ⁹⁰Y–¹⁷⁷Lu combination, both radionuclides (RN) simultaneously given in cocktail or successively in tandem, are now emerging (Frilling et al 2006, Seregni et al 2010, Kunikowska et al 2011, Villard et al 2012). They seem to confirm the previous results obtained in a rodent model. However, the used activity ratios of ¹⁷⁷Lu and ⁹⁰Y, 70–30% (Seregni et al 2010, Villard et al 2012) and 50–50% (Kunikowska et al 2011), were chosen on an empirical basis. Patient outcome should highly profit from an individualized combination of both radiopharmaceuticals (Savolainen et al 2012) . In addition, other RN with larger beta maximal ranges could be superior to ⁹⁰Y in combination with ¹⁷⁷Lu.

The purposes of this study are (i) to provide the dose-deposition kernel of ¹⁷⁷Lu (only ¹⁷⁷Lu 0.5 mm voxel-based S values have already been reported (Dieudonné et al 2010, Lanconelli et al 2012)) and also of long range beta-emitting RN, i.e. ¹⁴⁸Pm, ⁹⁰Y, ⁹³Y and ¹²⁵Sn, in order to allow easy voxel-based dose distribution calculation and (ii) to provide the tumour control probability (TCP) using these RN in combination with ¹⁷⁷Lu for several tumour models of different diameters including or not, heterogeneities of different sizes, and as recommended by Savolainen et al (2012), while keeping constant the biological effective dose (BED) to the renal cortex that is now widely recognized as the relevant parameter for the kidney toxicity (Barone et al 2005, Wessels et al 2008). A program computing these TCP for personalized parameters choice is also provided in the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia. These pieces of information should help those who would like to design further trials of combined RN therapy.

Dose-deposition kernel

Voxel dose distribution

Using a previously validated 3D convolution method (Lhommel et al 2010), the voxel (0.1 mm size on edge)-based dosimetry of the different RN was computed for different tumour models from the dose-deposition kernels derived as described above. Nine homogeneous active spherical tumours with diameters ranging from 1 to 25 mm were modelled. Four heterogeneous 25, 25, 25, 36 mm diameter active spherical tumours were modelled by including identical cold spheres of 1, 3, 5 and 7 mm diameter, respectively, set on the vertices of a cubic grid (figure 1). The distance between the vertices was three times the cold spheres radius so that the edge-to-edge distance between the cold spheres was equal to their radius, i.e. 0.5, 1.5, 2.5 and 3.5 mm, respectively. This ensures that the ratio between the volumes with, and without, RN uptake is almost independent of the heterogeneity size. A minimal distance equal to the cold spheres radius was kept between the edge of the cold sphere and the edge of the housing sphere. The housing sphere diameter was increased to 36 mm for the 7 mm heterogeneity in order to allow setting of more than one cold sphere.

Zoom In Zoom Out Reset image size

Voxel dose distribution of ⁹⁰Y, ⁹³Y, ¹⁴⁸Pm and ¹²⁵Sn in combination with ¹⁷⁷Lu

Three assumptions were made in all simulations: (i) tissue uptakes and pharmacokinetics expressed as a percentage of the activity injected to the patient are independent of the RN and of the labelled peptide, (ii) the specific activity in tumour voxels taking up the labelled compound is constant in the tumour and is independent of the tumour diameter and of the heterogeneity pattern, (iii) all the RN pharmacokinetics follow a mono-exponential time course with a biological half-life equal to the mean biological half-life of ⁸⁶Y-DOTATOC that was observed using amino acid infusion in a previously published phase I study in patients with neuroendocrine tumours (Jamar et al 2003), i.e. 210 and 92 h for the tumours and kidneys, respectively.

Different RN combinations were generated while keeping constant the renal cortex BED to 11 Gy per cycle that is one-third of the maximal renal cortex safe dose, which should be reached for the whole therapy (Wessels et al 2008). According to the activity measured ex vivo on a human kidney (Konijnenberg et al 2007), 70% and 30% of the total kidney activity were assumed to be in the cortex and in the medulla, respectively. Using these assumptions, the renal cortex dosimetry was assessed using the MIRD pamphlet no 19 kidney model (Bouchet et al 2003) included in OLINDA/EXM (Stabin et al 2005) . Table 1 shows, for the different RN, the effective half-lives in the tumour (T^tum_e1/2) and in the kidney (T^kid_e1/2) and the renal cortex dose $\bar D$, i.e. the absorbed dose per 1 MBq of the total activity in the kidney. The BED is

$$\begin{equation} {\rm BED} = D + \frac{\beta }{\alpha }GD^2 , \end{equation} \tag{ 1 }$$

where the Lea–Catcheside (McParland 2010) factor G is

$$\begin{equation} G = \frac{2}{D^2}\mathop \int \nolimits_0^{\infty} \,{\rm d}t\mathop \int \nolimits_0^t {\rm d}t^{\prime} \frac{{\rm d}D(t)}{{\rm d}t}\,{\rm e}^{ - \mu (t - t^{\prime} )} \frac{{{\rm d}D(t')}}{{{\rm d}t'}} \end{equation} \tag{ 2 }$$

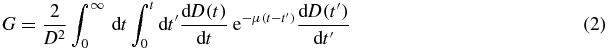
with α/β = 2.6 Gy for the quadratic model parameter and µ = ln(2)/2.8 h for the DNA enzyme repair rate of the glomerular cells (Barone et al 2005, Wessels et al 2008). Reading equation (2) from right to left, the absorbed dose rates $\frac{{{\rm d}D(t^\prime )}}{{{\rm d}t^\prime }}$ and $\frac{{{\rm d}D(t)}}{{{\rm d}t}}$ describe the probabilities that two independent particle tracks consecutively induce a DNA single-strand break at the times t' and t (t'<t). The exponential term ${\rm e}^{ - \mu (t - t^\prime )} ( \le 1)$ sandwiched in-between accounts for the probability that the enzyme system can repair the first DNA single-strand break before the second occurs, hence reducing the occurrence of a lethal DNA double-strand break. The double-integration handles that this scenario can occur at any time t' and t (t'< t). The absorbed dose rate for a combination with kidney activities A_R and A_L at t = 0 for the RN R and L is

$$\begin{equation} \frac{{{\rm d}D(t)}}{{{\rm d}t}} = \bar D_R A_R \lambda _R \,{\rm e}^{ - \lambda _R t} + \bar D_L A_L \lambda _L \,{\rm e}^{ - \lambda _L t} , \end{equation} \tag{ 3 }$$

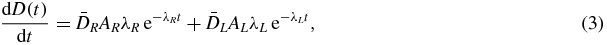
where λ = ln (2)/T^kid_e1/2 for each RN. The calculation of the BED using equations (1)–(3) gives a quadratic relation between the activities A_R and A_L in order to keep the BED constant. Using the previous assumptions, two expressions a^tum_R(x) and a^tum_L(x) can be found for the tumour-specific activities of the RN R–L combination x (0 ≤ x ≤ 1) keeping the BED constant (see the appendix).

Table 1. Tumour and kidney effective half-lives (in bold), and renal cortex dose $\bar D$ per MBq of total kidney activity (see 'Material and method').

	T1/2 decay (h)↓	Tumour Ttume1/2(h)	Kidney Tkide1/2(h)	Tumour/Kidney ratio	$\bar D$ (mGy/MBq)
T1/2 biol (h) →		210.0	92.0	2.28
93Y	10.2	9.7	9.2	1.06	27
90Y	64.2	49.1	37.7	1.30	89
148Pm	129.6	80.1	53.8	1.49	107
125Sn	232.2	110.3	65.9	1.67	139
177Lu	161.8	91.1	58.5	1.56	24

Tumour control probability

The TCP was computed using the formalism developed by Niemierko (1999) that includes two steps. The computation of the equivalent uniform dose (EUD):

$$\begin{equation} {\rm EUD} = \left( {\mathop \sum \limits_i v_i D_i^a } \right)^{{1} /{a}} , \end{equation} \tag{ 4 }$$

where v_i is the fraction of living cells that received an absorbed dose D_i. Afterward the TCP is computed by

$$\begin{equation} {\rm TCP} = \frac{1}{{1 + ( {{\rm TCD}_{50} /{\rm EUD}} )^{4\gamma _{50} } }}. \end{equation} \tag{ 5 }$$

TCD₅₀ is the tumour dose to control 50%, i.e. TCP = 0.5, of the tumours when they are homogeneously irradiated, γ₅₀ and a are unitless model parameters that are tumour specific. We used the values 60 Gy, 2 and −12 experimentally found by Gay and Niemerko (2007) for these parameters, respectively. In the computation of TCP using equations (4) and (5), the density of living cells was assumed to be constant in the tumour, even in the regions without uptake. However, the program provided in the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia allows changing this density, the Niemerko's parameters, and the kidney and tumour biological half-lives.

Disease control probability

Assuming that the disease of the patient is controlled only if his tumours are all controlled, we obtain

$$\begin{equation} {\rm DCP} = \mathop \prod \limits_i {\rm TCP}_i , \end{equation} \tag{ 6 }$$

where TCP_i is the TCP of the tumour i and the product is performed on all the tumours of the patient.

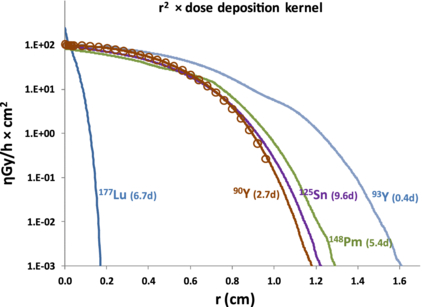
Figure 2 shows the dose-deposition kernels times the square of the distance r (this common representation well represents that at a distance r, a point is irradiated by a surrounding shell of area 4πr²). See the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia for numerical values of the ¹⁷⁷Lu, ⁹³Y, ¹⁴⁸Pm and ¹²⁵Sn dose kernels. For comparison, the ⁹⁰Y dose kernel computed by Cross et al (1992) using Monte Carlo was also shown (open circles).

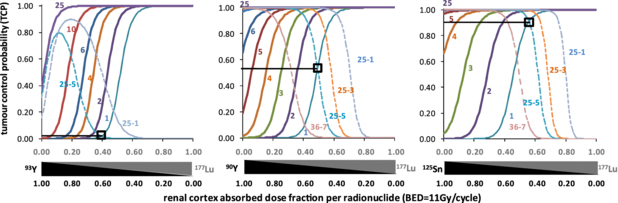
Zoom In Zoom Out Reset image size

Figure 3 shows the TCP as a function of the different RN combinations for a therapy course giving a constant renal cortex BED of 11 Gy per cycle. The tumour-initial-specific activities couple (a^tum_L(0), 0), i.e. 100% of ¹⁷⁷Lu, corresponding to a mean absorbed dose of 180 Gy to the homogeneous tumour of 25 mm in diameter for the whole therapy, i.e. ideally three cycles. Note that using ⁹⁰Y–¹⁷⁷Lu, homogeneous 2 mm tumour and 25 mm tumours with 3 mm heterogeneity can simultaneously be controlled (TCP > 0.9) using the combination providing a renal cortex absorbed dose with 50% originating from ¹⁷⁷Lu and 50% from ⁹⁰Y (as being quadratic, BED cannot be decomposed into two components). ¹²⁵Sn–¹⁷⁷Lu achieved a better result by simultaneously controlling homogeneous 1 mm tumour and tumours with 5 mm heterogeneity. ⁹³Y–¹⁷⁷Lu displayed the lowest TCP. The TCP obtained for this tumour-heterogeneity size couple were 0.02, 0.55 and 0.93 for ⁹³Y–¹⁷⁷Lu, ⁹⁰Y–¹⁷⁷Lu and ¹²⁵Sn–¹⁷⁷Lu respectively. ¹⁴⁸Pm provided results that were better than ⁹⁰Y but inferior to ¹²⁵Sn (data not shown).

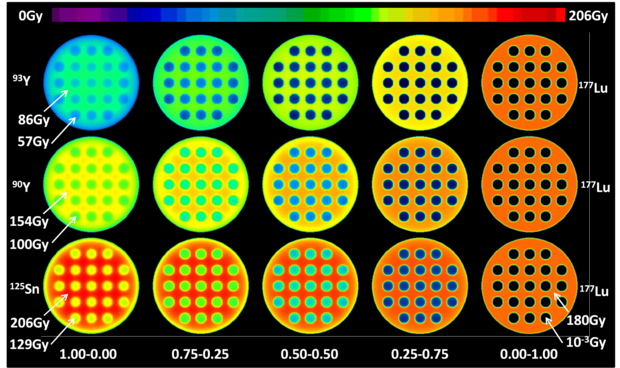
Zoom In Zoom Out Reset image size

Figure 4 shows the central slice of the voxel dose distribution for the 25 mm diameter sphere including 3 mm diameter cold spheres heterogeneity for the previous 180 Gy mean absorbed dose simulations. Pure ¹²⁵Sn provided the best irradiation of the inserted cold spheres and of the region between the cold spheres as well, while pure ¹⁷⁷Lu provided the best irradiation of the inner edge of the 25 mm diameter sphere. Note the increasing absorbed dose in the region between the cold spheres when ¹⁷⁷Lu is progressively replaced by ¹²⁵Sn, while keeping the renal cortex BED constant as a result of the longer ¹²⁵Sn decay half-life combined with the tumour washout that is slower to that of the kidney.

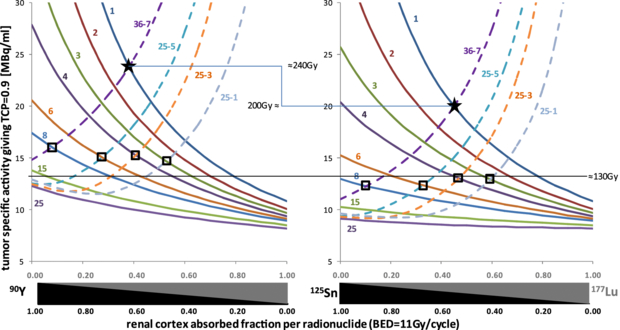
Zoom In Zoom Out Reset image size

Figure 5 shows the tumour-specific activity (in the area that takes up the RN) required when ¹⁷⁷Lu is injected alone in order to ensure a TCP of 90% for the different tumour models and for a therapy giving a constant renal cortex BED of 11 Gy per cycle. Regarding the tumour washout half-life and the ¹⁷⁷Lu beta energy, 15 MBq ml⁻¹ conveniently corresponds to about 150 Gy for ¹⁷⁷Lu alone (Stabin et al 2005). For a same tissue uptake, ¹²⁵Sn–¹⁷⁷Lu ensures a better simultaneous control of homogeneous and heterogeneous tumours. Using the appropriate RN proportions, ⁹⁰Y–¹⁷⁷Lu requires an additional uptake corresponding to 40 Gy than that required by ¹²⁵Sn–¹⁷⁷Lu to both controls 1 mm tumour and 7 mm heterogeneities. A program computing these curves for personalized choice of the Niemerko parameters, of the biological half-lives, of the threshold TCP, of the cell living density and of the therapy cycle BED is provided in the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia. When giving the therapy in one cycle with the maximal safe renal cortex BED, i.e. 33 Gy, the efficiency still improves a little bit in favour of ¹²⁵Sn–¹⁷⁷Lu (see the figure in the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia).

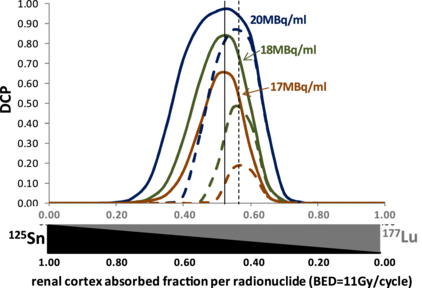
Zoom In Zoom Out Reset image size

Figure 6 shows the disease control probability (DCP) for different tumour-specific activities in a function of the ¹⁷⁷Lu–¹²⁵Sn combination proportions in two patients owning one 25 mm diameter tumour including 5 mm diameter heterogeneities jointly with one and ten 1 mm diameter homogeneous tumours, respectively. Due to the fast decrease of the TCP in heterogeneous tumours (see figure 3), only a small shift of the optimal combination proportions in favour of ¹⁷⁷Lu is observed for the patient burdened with ten 1 mm tumours. However, for this patient the maximal DCP decreases faster with the tumour-specific activity. The program provided allows computing DCP for personalized number of tumours.

Zoom In Zoom Out Reset image size

The simple, but challenging, tumour model studied here clearly shows the benefit of using ⁹⁰Y–¹⁷⁷Lu combination rather than a single RN alone. This is in line with the experimental observations of de Jong et al (2005). The combination providing a 50–50 renal cortex absorbed dose originating from ¹⁷⁷Lu and ⁹⁰Y appears to be a good compromise: for a mean tumour delivered dose of 180 Gy, this combination simultaneously allows controlling small homogeneous tumours down to 2 mm diameter, as well as heterogeneities up to 3 mm diameter. This combination expressed as a fraction of RN activities to inject corresponds to a 75% ¹⁷⁷Lu–25% ⁹⁰Y cocktail. This is close to the combination used by Seregni et al (2010) , but is quite different from the 50–50% tandem used by Kunikowska et al (2011). For a tumour mean delivered dose of 180 Gy, this last proportion controls 7 mm heterogeneities, but not tumours smaller than 5 mm in diameter.

For the time being, ⁹⁰Y is not yet proposed in combination with ¹³¹I internal radiotherapy. ¹³¹I owning a beta range and a half-life almost similar to those of ¹⁷⁷Lu, the previous considerations are expected to be valid for ⁹⁰Y combination therapy with ¹³¹I. Bone marrow toxicity was not addressed here; however, knowing the bone marrow pharmacokinetics for the different RN, the present methodology could be applied by studying the combination proportions that keep the most critical tissue, i.e. renal cortex or bone marrow, to its maximal safe BED. Note that this most critical tissue could change when moving from pure ¹⁷⁷Lu to pure ⁹⁰Y (or ¹²⁵Sn) proportion.

The results also show that there is no significant difference between a tumour mean absorbed dose of 130 and 200 Gy when a single RN is used: for both absorbed doses, ⁹⁰Y cannot control tumours smaller than 6 mm, and for both absorbed doses, ¹⁷⁷Lu controls all homogeneous tumours, but not heterogeneity (figure 5(left)). On the other hand, using a RN combination, the situation dramatically changes between these two absorbed doses: 130 Gy can only control 6 mm tumours and 1 mm heterogeneity together, while 200 Gy can simultaneously control 1 mm tumour and 5 mm heterogeneity. As the ⁸⁶Y-SMT-487 trial showed huge differences in renal uptake (Barone et al 2005, Jamar et al 2003), it is of paramount importance to individually assess this uptake to inject the most efficient safe dose to each patient. Of course, this uptake should be evaluated separately for each RN. ¹⁷⁷Lu is easily imaged by SPECT, and the ⁹⁰Y uptake can be accurately assessed after the first therapy cycle either by PET (Walrand et al 2010) or by bremsstrahlung pinhole SPECT (Walrand et al 2011). In addition, curves of figure 5 can be individually computed from patient-specific tumour and kidney dosimetry using the program provided in the online supplementary material available at stacks.iop.org/PMB/57/4263/mmedia. This may allow assessing the individual optimal RN proportions.

Despite its large beta range (17 mm), ⁹³Y performed less well than ⁹⁰Y. This is linked to its short half-life (10 h) that does not enable to benefit from the differential washout between the kidney and the tumours (table 1). The same behaviour was noted for ⁶⁶Ga (30 mm, 9.5 h) and ⁷²Ga (19 mm, 14 h) (data not shown). Note that in the case of ⁹³Y, the comparison is entirely valid due to its identical chemical properties to those of ⁹⁰Y or ⁸⁶Y. The comparison will have to be refined for ¹²⁵Sn when biodistribution and pharmacokinetics can be assessed.

After making these observations, we searched using the LNBL isotopes tool (see footnote ²) and analyse the beta spectrum of RN with a half-life longer than that of ⁹⁰Y and with a beta end point energy higher than 1.7 MeV. Nine RN came out from this search (table 2), including only two RN, ¹⁴⁸Pm and ¹²⁵Sn, still having a significant beta abundance of end point energy up to 2 MeV. However, ¹²⁵Sn had a significantly longer half-life and performed not only better than ⁹⁰Y, but also better than ¹⁴⁸Pm (data not shown). As expected ¹²⁵Sn provided the best tumour control: for 180 Gy, 1 mm tumour and 5 mm heterogeneities can be controlled (figure 3). Furthermore, for 200 Gy 1 mm tumour and 7 mm heterogeneities can be simultaneously controlled (figure 5(right)).

¹²⁵Sn has the drawback to decay into a beta emitter: ¹²⁵Sb (2.7 years) that afterwards decays to the stable isotope ¹²⁵Te. The total ¹²⁵Sb activity produced will be 1% of the ¹²⁵Sn activity (half-life ratio 232 h/2.7 years). Due to the long ¹²⁵Sn half-life (232 h) compared to the kidney washout half-life (92 h), only a small part of the ¹²⁵Sn will decay into ¹²⁵Sb in the kidney. For the time being, the exact computation of the additional irradiation induced by the progeny ¹²⁵Sb is not possible owing to the fact that pharmacokinetics of ¹²⁵Sn-labelled peptides were not assessed yet. However, even if all the ¹²⁵Sb produced in the kidney is retained, a simple computation shows that ¹²⁵Sb will only give a maximal additional kidney absorbed dose of 10% than that given by ¹²⁵Sn. ^117mSn-DTPA has been used in bone pain palliation (Bishayee et al 2000) and has shown a good stability in vitro and in vivo (Srivastava et al 1985). Peptide labelling with ¹²⁵Sn is thus likely feasible.

¹²⁵Sn is a fission product, but can also be produced by fast or thermal neutrons irradiation of the stable isotope ¹²⁴Sn in the same way as ¹⁷⁷Lu. ¹²⁵Sn for the time being has no application and was produced only in small amounts for the fundamental nuclear physics research. Natural tin is a mix of the stable isotopes ^{112,114–120,122,124}Sn. However, irradiation of ¹²⁴Sn-enriched targets (Krane and Sylvester 2006, Mayer et al 1992) by thermal neutron, followed by 10 days cooling, produces ¹²⁵Sn almost free of other radioisotopes (<1%). However, cross sections appear limited for a medical production. Table 3 shows the typical ¹²⁵Sn activity produced in the ⁹⁹Mo/^99mTc generator manufacturing by thermal neutron irradiation of ²³⁵U (Mushtaq et al 2009). Tin RN can be rapidly extracted and purified from the fission products (Erdal and Wahl 1968). The short half-lived ^121,127,128Sn can be removed by physical decay, the other beta emitter contaminants to be taken into account in the therapy dosimetry planning.

The present simple tumour model showed the benefit of ¹²⁵Sn–¹⁷⁷Lu versus ⁹⁰Y–¹⁷⁷Lu. However, the determination of the optimal combination proportion for clinical therapy requires more realistic tumour modelling. Unfortunately, heterogeneity of neuroendocrine tumours in humans is different from preclinical therapy model (Marcos et al 2002) and up to now structural and RN imaging at cellular level can be obtained only by ex vivo techniques. Tumour RN distribution depends not only on the receptor density distribution as shown by autoradiography after ex vivo incubation with the labelled peptide but also depends on the vascular tumour system. Direct data from patients injected with ¹¹¹In-octreotide would be extremely useful to further explore this avenue and obtain realistic tumour heterogeneity models. Finally, proposed refinement of TCP calculation (Hobbs et al 2011) to account for statistical fluctuations associated with low activities should be considered.

This study strongly supports the merit to perform clinical trial using the ⁹⁰Y–¹⁷⁷Lu combination with a RN proportion optimized from a patient-specific tumour and kidney dosimetry. The latter point is of prime importance in order to inject the most efficient safe activity with the optimal RN proportion in view of the fact that a small reduction of the tumour absorbed dose can drastically knock down the tumour control. This study confirms that ⁹⁰Y is a good RN that can easily be used in combination with ¹⁷⁷Lu.

According to published data, production of ¹²⁵Sn and its coupling to somatostatin analogue appear feasible. From a physical viewpoint, ¹²⁵Sn is the best RN for internal radiotherapy in combination with ¹⁷⁷Lu and provides significantly better tumour control than using ⁹⁰Y. This result is based on the assumption that the pharmacokinetics of peptides labelled with ⁹⁰Y and ¹²⁵Sn are similar. It is thus of prime importance to challenge this assumption. The first step should be to assess the biodistribution and pharmacokinetics of ¹²⁵Sn-labelled somatostatin analogues in rodents. The same concept can be applied to other human tumour models known to contain large heterogeneities. Finally, the biological behaviour of its progeny ¹²⁵Sb has also to be assessed in order to refine the simulation of the radioprotection issues.

The absorbed dose is

$$\begin{equation} D = \mathop \int \nolimits_0^\infty {\rm d}t\frac{{{\rm d}D(t)}}{{{\rm d}t}} = \bar D_R A_R + \bar D_L A_L . \end{equation} \tag{ A.1 }$$

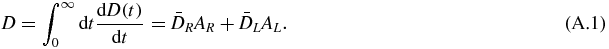
The double integration in equation (2) gives

$$\begin{eqnarray} &&\fl {\rm BED} = \bar D_R A_R + \bar D_L A_L + \frac{\beta }{\alpha }\bigg( \bar D_R^2 A_R^2 \frac{{\lambda _R }}{{\lambda _R + \mu }} + 2\bar D_R A_R \bar D_L A_L \frac{{\lambda _R \lambda _L }}{{\lambda _R + \lambda _L }}\bigg( {\frac{1}{{\lambda _R + \mu }} + \frac{1}{{\lambda _L + \mu }}} \bigg)\nonumber\\ &&+\, \bar D_L^2 A_L^2 \frac{{\lambda _L }}{{\lambda _L + \mu }} \bigg). \end{eqnarray} \tag{ A.2 }$$

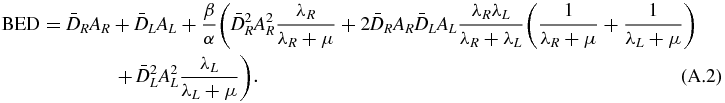
Equation (A.2) can be rewritten as

$$\begin{equation} aA_L^2 + bA_L - c = 0, \end{equation} \tag{ A.3 }$$

with

$$\begin{equation} a = \frac{\beta }{\alpha }\bar D_L^2 \frac{{\lambda _L }}{{\lambda _L + \mu }}, \end{equation} \tag{ A.4 }$$

$$\begin{equation} b(A_R ) = \bar D_L + \frac{\beta }{\alpha }\left( {2\bar D_R A_R \frac{{\lambda _R \lambda _L }}{{\lambda _R + \lambda _L }}\left( {\frac{1}{{\lambda _R + \mu }} + \frac{1}{{\lambda _L + \mu }}} \right)} \right)\bar D_L , \end{equation} \tag{ A.5 }$$

$$\begin{equation} c({\rm BED},A_R ) = {\rm BED} - \bar D_R A_R - \frac{\beta }{\alpha }\bar D_R^2 A_R^2 \frac{{\lambda _R }}{{\lambda _R + \mu }}. \end{equation} \tag{ A.6 }$$

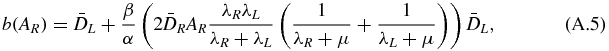
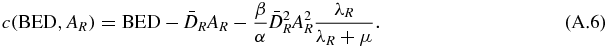
As a, b and c are positive, the solution of equation (A.3) is

$$\begin{equation} A_L ({\rm BED},A_R ) = \frac{{ - b(A_R ) + \sqrt {b^2 \left( {A_R } \right) + 4ac({\rm BED},A_R )} }}{{2a}}. \end{equation} \tag{ A.7 }$$

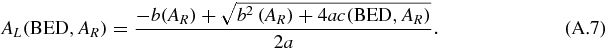
Let start with a combination composed by 100% of the RN L = ¹⁷⁷Lu, i.e. A_R = 0. The ¹⁷⁷Lu activity Al that gives a kidney BED to the cortex is A_L(BED, 0). Then, equation (A.7) gives the activity of ¹⁷⁷Lu in the combination in order to keep BED constant when the activity of the RN R is progressively increased up to A^max_R, i.e. A_L(BED, A^max_R) = 0.

Let assume that for this combination composed by 100% of the RN L = ¹⁷⁷Lu, the tumour-initial-specific activity is a^tum_L. Then, resulting from assumption (i) the tumour-specific activity couple (a^tum_L, a_R^tum) at t = 0 of the RN combination x giving the kidney activity couple (A_L(BED, xA^max_R), xA^max_R) at t = 0 to the kidney with 0 ≤ x ≤ 1 is given by

$$\begin{equation} a_L^{{\rm tum}} (x) = A_L ({\rm BED},xA_R^{{\rm max}} )\frac{{a_L^{{\rm tum}} }}{{A_L ({\rm BED},0)}}, \end{equation} \tag{ A.8 }$$

$$\begin{equation} a_R^{{\rm tum}} (x) = xA_R^{{\rm max}} \frac{{a_L^{{\rm tum}} }}{{A_L ({\rm BED},0)}}. \end{equation} \tag{ A.9 }$$

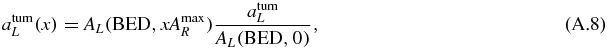
Note that in the combination made of 100% of the RN R, a^tum_R(1) can be greater or smaller than a^tum_L depending on the decay properties of the RN R.