Abstract
Suppose, in contrast to the fact, in 1950, we had put the cohort of 18-year-old non-smoking American men on a stringent mandatory diet that guaranteed that no one would ever weigh more than their baseline weight established at the age of 18 years. How would the counterfactual mortality of these 18 year olds have compared to their actual observed mortality through 2007? We describe in detail how this counterfactual contrast could be estimated from longitudinal epidemiologic data similar to that stored in the electronic medical records of a large health maintenance organization (HMO) by applying g-estimation to a novel of structural nested model (SNM). Our analytic approach differs from any alternative approach in that, in the absence of model misspecification, it can successfully adjust for (i) measured time-varying confounders such as exercise, hypertension and diabetes that are simultaneously intermediate variables on the causal pathway from weight gain to death and determinants of future weight gain, (ii) unmeasured confounding by undiagnosed preclinical disease (that is, reverse causation) that can cause both poor weight gain and premature mortality (provided an upper bound can be specified for the maximum length of time a subject may suffer from a subclinical illness severe enough to affect his weight without the illness becomes clinically manifest) and (iii) the presence of particular identifiable subgroups, such as those suffering from serious renal, liver, pulmonary and/or cardiac disease, in whom confounding by unmeasured prognostic factors is so severe as to render useless any attempt at direct analytic adjustment. However, (ii) and (iii) limit the ability to empirically test whether the SNM is misspecified. The other two g-methods—the parametric g-computation algorithm and inverse probability of treatment weighted estimation of marginal structural models—can adjust for potential bias due to (i) but not due to (ii) or (iii).
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Willett WC, Dietz WH, Colditz GA . Guidelines for healthy weight. N Engl J Med 1999; 341: 427–434.
Robins JM . Estimation of the time-dependent accelerated failure time model in the presence of confounding factors. Biometrika 1992; 79: 321–334.
Robins JM, Wasserman L . Estimation of effects of sequential treatments by reparameterizing directed acyclic graphs. In: Geiger D, Shenoy P (eds). Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence, Providence Rhode Island, 1–3 August 1997. Morgan Kaufmann: San Francisco, 1997, pp 409–420.
Robins JM . Association, causation, and marginal structural models. Synthese 1999; 121: 151–179.
Robins JM, Hernan MA, Siebert U . Effects of multiple interventions. In: Ezzati M, Lopez AD, Rodgers A, Murray CJL (eds). Comparative Quantification of Health Risks: Global and Regional Burden of Disease Attributable to Selected Major Risk Factors, vol I. World Health Organization: Geneva, 2004, pp 2191–2230.
Hernán MA, Hernandez Diaz S, Robins JM . A structural approach to selection bias. Epidemiology 2004; 15: 615–625.
Robins JM . Correcting for non-compliance in randomized trials using structural nested mean models. Commun Stat 1994; 23: 2379–2412.
Robins JM . Optimal structural nested models for optimal sequential decisions. In: Lin DY, Heagerty P (eds). Proceedings of the Second Seattle Symposium on Biostatistics. Springer-Verlag: New York, 2004.
Robins JM . Causal inference from complex longitudinal data. In: Berkane M (ed). Latent Variable Modeling and Applications to Causality. Lecture Notes in Statistics (120). Springer-Verlag: New York, 1997, pp 69–117.
Murphy SA . Optimal dynamic treatment regimes. J R Stat Soc Ser B 2003; 65: 331–366.
Robins JM, Scharfstein D, Rotnitzky A . Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models. In: Halloran ME, Berry D (eds). Statistical Models in Epidemiology: the Environment and Clinical Trials. Springer-Verlag: New York, 1999, pp 1–94.
Lok JJ, Gill RD, van der Vaart AW, Robins JM . Estimating the causal effect of a time-varying treatment on time-to-event using structural nested failure time models. Stat Neerl 2001; 58: 271–295.
Robins JM . General methodological considerations. J Econom 2003; 112: 89–106.
Robins JM . Testing and estimation of direct effects by reparameterizing directed acyclic graphs with structural nested models. In: Glymour C, Cooper G (eds). Computation, Causation, and Discovery. AAAI Press/The MIT Press: Menlo Park, CA; Cambridge, MA, 1999, pp 349–405.
Robins JM . Analytic methods for estimating HIV treatment and cofactor effects. In: Ostrow DG, Kessler R (eds). Methodological Issues of AIDS Mental Health Research. Plenum Publishing: New York, 1993, pp 213–290.
Joffe MM, Hoover DR, Jacobson LP, Kingsley L, Chmiel JS, Fischer BR et al. Estimating the effect of Ziduvodine on Kaposi's sarcoma from observational data using a rank preserving failure time model. Stat Med 1998; 17: 1073–1102.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
A formal definition of a joint SNFTM for Xm and a SNMM for Ym∣Xm
The definition here is the alternative, more intuitive and more general definition mentioned in the main text. The equivalence with the definitions in the main text is proved below.
We first consider the uncensored case. The observed data are 
, X, Y, where X is a continuous time to event variable and Y is measured at K+1. The counterfactual data are (Xm, Ym), m=0, …, K+1, denoting X and Y under treatment regimens where one experiences his observed treatment 
up to m and then receives no treatment (treatment level 0) thereafter. We make the assumption that XK+1=X, YK+1=Y. The covariate L(k) precedes A(k) which precedes L(k+1).
The function 
is a counterfactual conditional quantile–quantile function, where S and S−1 denote a survivor function and its inverse. It is a standard result that xm†(x, 
) is the unique function for which 
, 
) and Xm have the same conditional distribution, that is,
Define XK+1†=X and then recursively define Xm†≡xm†(Xm+1†, 
). Robins and Wasserman3 proved the following
Theorem A1:
where we silently take such equations to hold for all m=0, …, K.
Furthermore, Robins and co-workers11, 14 and Lok12 proved the function xm† is unique. That is if the above equation holds for with Xm† replaced by some Hm=hm(Hm+1, 
) and HK+1=X, then the function hm must be the function xm†.
An SNFTM for Xm assumes
for a known function xm(x, 
; ψ) satisfying xm(x, 
, ψ)=x if ψ=0 or A(m)=0 with ψ* an unknown parameter vector.
It follows immediately that
with
The uniqueness of Xm† implies that SNFTMs as defined in the text are also SNFTMs as defined here.
Recall 
, 
) and define
which is equivalent to
Define YK+1†=Y and then recursively define Ym†=Ym+1†−γm†( 
, Xm†).
We prove the following theorem below.
Theorem A2:
Furthermore the function γm† is unique. That is if the above equation holds with Ym† replaced by some Hm=Hm+1−hm( 
, Xm†) and HK+1=Y, then the function hm must be the function γm†.
An additive SNMM for Ym∣Xm assumes
for a known function γm( 
, x; β) satisfying γm( 
, x; β)=0 if β=0 or A(m)=0 with β* an unknown parameter vector.
It follows immediately that
with
The uniqueness of γm† implies that an additive SNMM for Ym∣Xm as defined in the text is equivalent to the additive SNMM for Ym∣Xm as defined here.
Proof of Theorem A2: By backward induction.
Case 1: m=K;
where the first equality uses the definition of YK† and that YK+1=Y=YK+1†, the second uses that 
by XK+1=X=XK+1†, and the third is the definition of γK†(Ā(K), 
.
Case 2: Assume true for m. We prove true for m+1.
(by the laws of probability)
(by the induction assumption)
(by 
and 
having identical distributions)
(by the laws of probability) 
(by the definition of 
)
(by the defintion of 
Uniqueness is proved as in Robins8 and Lok et al.12 and is omitted.
An additive SNMM for Ym∣Xm may not be appropriate for analyzing censored data due to administrative censoring of X at time K as discussed in the text. As indicated in the section Censoring, our approach requires that we consider a broader class of SNMM models, which we now describe.
Consider a collection of functions cm†(x, 
) indexed by m and define 
and 
. For fixed 
, cm†(x, 
) need not be a 1–1 function of x.
Redefine
which is equivalent to
Define YK+1†=Y and then recursively redefine Ym†=Ym+1†−γm†( 
, Cm†). We have the following theorem.
Theorem A3:
Furthermore the function γm† is unique. That is, if the above equation holds with Ym† replaced by some Hm=Hm+1−hm( 
, Cm†) and HK+1=Y, then the function hm must be the function γm†.
Proof of A.3: We only describe where the proof differs from that of its special case Theorem A.2. The proof is essentially identical except for the replacement of Xm by Cm, x by c and 
by
An additive SNMM for Ym∣Cm assumes
for a known function γm( 
, c; β) satisfying γm( 
, c; β)=0 if β=0 or A(m)=0 with β* an unknown parameter vector.
Then given a SNFTM 
for Xm and a function 
that may depend on the functions 
j⩾m, suppose we can define a parametrized class of functions 
satisfying
For example, in the section on censoring in the main text, we took 
Then defining 
we have
with
Appendix 2
Estimation of effects with the parametric g-formula and IPTW when a sufficiently long MLP exists
In this section, we show that the parametric g-formula and IPTW can be used to estimate certain causal effects when there exists a sufficiently long MLP. We begin with a preliminary discussion of these two methods of estimation.
Preliminaries. In this preliminary discussion, we assume that, as in the section A locally rank-preserving SNM, there is neither confounding by preclinical disease nor an MLP. Specifically we assume, for each regimen g, the COg assumption that, for each j, 
holds, with Ξg(m) defined in Equation (53).
Recoding: Without loss of generality, we henceforth redefine (that is, recode) 
such that Ξg(j) is now one of the components of 
but we remove from 
the components corresponding to X, that is, the components (XI(X⩽j), I(X⩽j)). Then we can write the COg assumption as
as, from these definitions, Ξg(j)=0 implies AΔg(j)=0. The COg assumption implies
as 
implies (Yjg, Xjg)=(Y0g, X0g). This last equation is the standard definition of no unmeasured confounding given (
, (XI(X⩽j), I(X⩽j))) for the effect of AΔg(j) on the counterfactuals Y0g, X0g. Let 
be the conditional hazard of X given the information in •.
Robins4, 15 proves that Equation (74) implies that
is identified through
with
where the first formula for 
is referred to as the g-computation algorithm formula (g-formula, for short) and the second formula as the IPTW formula. To shorten the formulae, we have written 
as a shorthand for 
when the time t is clear. In fact Robins4, 15 shows that the assumption
which is implied by the assumption of Equation (74), suffices to establish the identifying formulae. To estimate 
, we can use either the parametric g-formula estimator that replaces the unknowns 
and 
in the first formula by estimates based on parametric models or the IPTW estimator that replaces the unknown 
in the second formula with a parametric estimate and the unknown expectation with a sample average. Both approaches are alternatives to g-estimation of structural nested models (SNMs).
Robins4, 15 proves E[Y0g] is identified under the assumption of Equation (74) by
In the above formulae, we have assumed for simplicity that X has support on (0, K+1) so censoring for X is absent.
We next consider whether 
and E[Y0g] remain identified in the presence of confounding by preclinical disease and a sufficiently long MLP.
Identification and estimation of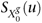 
The following theorem establishes the identification of 
First note under our recoding, the RCg assumption becomes
Theorem A4: Given a regimen g, let a g-specific MLP satisfy the definition of an MLP of the section Estimation under a rank-preserving SNM for Ym∣Xm with Xm known, except with Xk and Xm replaced by Xkg and Xmg and A(m) replaced by AΔg(m). Suppose AΔg(m) has a g-specific MLP of χ months for its effect on X where χ exceeds the time ς in the CDg assumption. Then, under the CDg and RCg assumptions, 
remains identified by both the g-formula and the IPTW formula when the recoded L(t) and AΔg(t) are redefined as L†(t) and AΔg,†(t) where
The theorem thus states that the identifying formulae are the usual g-formula and IPTW formula except we replace both the treatment variable AΔg(t) and the covariate variable L†(t) by their values χ time units earlier. (For the IPTW formula, the transformation is applied to 
It is important to emphasize that a similar transformation is not applied to X. Thus, the conditioning event 
transforms to 
.
Proof of theorem: It suffices to show Equation (78) holds when L(t) and AΔg(t) are replaced by L†(t) and AΔg,†(t). By RCg, 
Thus, 
By CDg and χ>ς, 
Thus 
with m≡χ+j.
Now the event X>(m−χ) is the event Xm−χg>(m−χ). Further, by χ a g-specific MLP we also have the event Xm−χg>m is the event X>m. Thus, we have 
As, given 
we have (Ym−χg, Xm−χg)=(Y0g, X0g), we conclude 
, which is exactly Equation (78) with L(t) and AΔg(t) replaced by L†(t) and AΔg,†(t), proving the theorem.
In contrast, under the conditions of the previous theorem, E[Y0g] is not identified because Equation (74), in contrast to Equation (78), fails to hold when L(t) and AΔg(t) are replaced by L†(t) and AΔg,†(t). Specifically, Equation (74) can be written as the conjunction of Equation (78),
and
We show below that under the conditions of the previous theorem, Equation (81) holds but Equation (82) does not when L(t) and AΔg(t) are replaced by L†(t) and AΔg,†(t) To show (81) we modify slightly the proof of Equation (78) as follows:
by the g-specific MLP assumption.
The proof of (82) fails because the event 
is not the same event as 
, under CDg because Xjg<j+ς does not imply 
Proof that E[YT0] is non-parametrically identified when a sufficiently long MLP exists. In the section Intractable confounding in subgroups, we stated that E[YT0] is non-parametrically identified under the conditions of the previous theorem with the regimen g in the theorem being the regimen that always assigns exposure zero. A proof follows.
Let IN, AT, ΞT, YTm, XTm be as defined in the section Intractable confounding in subgroups where we recall that because of the existence of the MLP of length χ>ς, all subjects with ς<Xm<m+ς have IN(m)=1. First in Equations (78), (81) and (82) we replace (Y0g, X0g) by (YT0, XT0), AΔg(m) by AT(m−χ), and redefine L(m) as L(m−χ) with the component Ξ(m) of L(m) being replaced by ΞT(m−χ). Equation (82) now holds trivially because with probability one m−χ+ς>X implies IN(m−χ)=1 and thus ΞT(m−χ)=0 and AT=(m−χ)=0. Furthermore, the proofs of Equations (78) and (81) go through as above with only minor notational changes. We therefore conclude that Equation (74) holds and thus that E[YT0] is non-parametrically identified. The identifying IPTW formula is explicitly given by
Appendix 3
Optimal regimen models
Suppose we now wish to estimate the regimen gopt that maximizes E[Y0g] over all regimens g. We will do so by specifying an optimal regimen SNMM and associated SNFTM.
To begin consider the dietary intervention a(k), gopt,k+1 in which one follows his observed diet up to month k, allows a BMI increase of a(k) over his maximum previous BMI in month k, and follows the unknown optimal regimen gopt thereafter. Let 
be the associated counterfactuals. When A(k)=a(k), write gopt,k+1 for the regimen A(k), gopt,k+1. Note 
We will make the following assumptions:
Optimal regimen RC assumption: A(m) is statistically independent of 
given Ξ(m)=1, 
and 
for each a(m)⩾0.
Optimal regimen CD assumption:
We next recursively define random variables 
by the relationship that 
and, for m=K, … 0,
These equations recursively define 
in terms of the observed data, the regimen gopt,m+1 and the parameter vector ψ as can be verified by noting that these equations imply the following relationship between 
and 
We assume an optimal regimen SNFTM given by
for an unknown value ψ* of the vector ψ.
We also assume an optimal regimen SNMM
Above ω(a(t), ā(t−1), l̄(t), ψ) and γm[a(m), ā(m−1), l̄(m), x, β] are known functions satisfying ω(a(t), ā(t−1), l̄(t), ψ)=0 if a(t)=0 or ψ=0 and γm(a(m), ā(m−1), l̄(m), β)=0 if a(m)=0 or β=0.
The optimal regimen itself remains unknown. However, we show below that the following algorithm evaluated at the true (β*, ψ*) would find the optimal regimen gopt under the following additional condition, that we henceforth assume to hold.
Additional condition: For each ā(m−1), l̄(m), x, β, m the function γmopt[a(m), ā(m−1), l̄(m), x, β] is either everywhere zero or is strictly concave downward in a(m) on the support of A(m).
Optimal regimen algorithm: Given any (β, ψ), calculate 
as follows.
Calculate 
Define
Calculate
Calculate 
Recursively for m=K−1, … 0, calculate 
Calculate 
Calculate
Note that to carry out this algorithm we will need to be able to estimate
for all possible values of a(m) in support of A(m). One possibility is to specify and fit an appropriate multivariate regression model with the possible values of a(m) indexing the multivariate outcomes at time m.
To understand why this is the correct algorithm, we first note that any regimen at m can be a function of X only if X⩽m, so that X is known by m. When X>m, we must average over 
because 
is a function of X. When X>m, 
will be the value of 
if the optimal regimen gopt(β,ψ) dictates the exposure a(m). The optimal regimen will choose the a(m) that optimizes the contribution to the utility at time m. But the optimizing a(m) depends on the a(k) chosen for the regimen for k>m. Thus, we need to use backward recursion to estimate the optimal regimen.
To be more specific, consider the subgroup of subjects with a history 
with X<K so 
Then 
that maximizes 
is the optimal treatment choice at K. However, we are only considering regimens (interventions) that do not force subjects to gain weight. We now argue that for any subject with A(K) less than 
the optimal decision is not to intervene at all, so the subject receives his observed treatment A(K). The subject with A(K) less than 
could still have received any treatment between 0 and A(K). However, among these set of treatments, the treatment A(K) is optimal by the concavity condition above.
Next consider the subgroup of subjects with a history (
with X>K. To find the optimal treatment, we average over 
. As the average over 
of a function that is concave in a(K) for every possible value of 
remains a concave function of a(K), we again take 
That the same argument holds for each m is a standard dynamic programming argument as discussed in Robins.8
As (β*, ψ*) are unknown we must estimate them by g-estimation. Define
Note these equations are much more complex than the equations for ψ using an SNFTM and SNMM for a fixed g in that gopt is now not known but depends on the parameters (β, ψ) through the above algorithm for gopt(β, ψ). Thus, we can no longer estimate ψ* independently of β* as 
is now a function of β as well as ψ through its dependence on gopt(β,ψ). Rather, we must solve both pairs of g-estimation equations simultaneously.
Specifically, given the optimal regimen RC and CD assumptions, to obtain CAN estimators of the unknown parameters, we find jointly (
) so that both the score test for the covariate vector depending on 
is precisely zero and the score test for the covariate vector depending on 
is precisely zero (both tests are restricted to subjects with 
and Ξ(m)=1). This turns out to be a very difficult computational problem. Robins8 describes a number of computational simplifications, but they are beyond the scope of the current paper. Finally, we obtain 
as our estimate of the optimal regimen gopt(β*,ψ*) and 
as our estimate of the expected utility 
under the optimal regimen.
Both estimation of E[Y0g] for a known g and of 
can be modified to allow for censoring at the end of follow-up at K+1 and for intractable unmeasured confounding in certain subgroups using methods exactly analogous to the methods for the estimation of E[Y0].
Rights and permissions
About this article
Cite this article
Robins, J. Causal models for estimating the effects of weight gain on mortality. Int J Obes 32 (Suppl 3), S15–S41 (2008). https://doi.org/10.1038/ijo.2008.83
Published:
Issue Date:
DOI: https://doi.org/10.1038/ijo.2008.83
Keywords
This article is cited by
-
Association Between Body Mass Index Variation and Early Mortality Among 834 Ethiopian Adults Living with HIV on ART: A Joint Modelling Approach
Infectious Diseases and Therapy (2023)
-
Quantifying causal effects from observed data using quasi-intervention
BMC Medical Informatics and Decision Making (2022)
-
Association between cardiovascular risk-factors and venous thromboembolism in a large longitudinal study of French women
Thrombosis Journal (2021)
-
Protocol: Adaptive Implementation of Effective Programs Trial (ADEPT): cluster randomized SMART trial comparing a standard versus enhanced implementation strategy to improve outcomes of a mood disorders program
Implementation Science (2014)
-
Workshop on estimating the health burden of overweight and obesity
International Journal of Obesity (2008)
