Introduction

Navigation is widely used in ENT surgery to support the surgeon. A crucial part of the whole navigation process is the registration of the patient to the preoperative CT/MRI images. Usually paired-point matching [1,2,3] or more recently surface registration [4, 5] is used for registration. Homologous points on the patient and in the image (fiducials) are used to find the rigid transformation between them. Errors in localizing fiducials in image and patient space FLE lead to the FRE [6], which is the Euclidean distance between the corresponding fiducials after registration. Usually, fiducials on the surface of the patient are used for registration, but the operating area is inside the head. Tracking errors and errors in localizing fiducials on the patient or in the images prohibit perfect navigation. The TRE [6] allows surgeons estimating the accuracy of navigation inside the patient at the surgical target zone. This is thus a good measure for the theoretical clinical application accuracy of a navigation system. Knowing TRE before surgery is a key component for a reliable intraoperative use of information guidance provided by navigation systems. The use of CAS systems might improve surgery, reduce peri- and postoperative complications, and thus might allow faster healing of patients [7]. Therefore, a prediction of the error in special regions inside the head, especially close to critical structures, is highly desirable. Different prediction methods for TRE were developed [6, 8,9,10,11]. From a clinical perspective good predictions should overestimate the real application error.

Theoretical comparisons [12], numerical simulations [6, 8,9,10,11], and clinical studies [13,14,15] tried proving the methods for predicting TRE. To the best of our knowledge, a comprehensive analysis of available prediction methods of application accuracy against experimental data in a surgical setup is not available yet.

The first raw analysis of the data presented in this paper has already been published in [16], where only isotropic registration with an isotropic FLE model was investigated. The present work extends [16] with a comprehensive analysis of the data by including isotropic and anisotropic errors of measurements, registrations, and prediction methods. The emphasis is on the most frequently used prediction method [6] or methods that fit the simulated surgery best: anisotropic prediction [8] and a general approach [10]. This investigation presents a critical appraisal of predictions and measurements for computer-assisted navigation, based on real data from experiments collected under realistic conditions.

Numerical simulations of the experiment that by definition fulfill all theoretical requirements served to compare purely theoretical predictions against predictions on base of experimental data. For both “experiments” statistical correlations between measured and predicted quantities (such as TRE) were calculated. For the simulated data also distributions of the measured and predicted errors were analyzed. The specific advantage of both experiments (numerical and real life) is that ALL positions in patient and image spaces, including target positions, are available and can be used for relevant calculations and measurements.

The next sections describe the data acquisition, all errors, measured and predicted, are defined, and the whole experiment is described. In the final sections, the results are presented and discussed.

Materials and methods

Data acquisition

For the experiments a plastic skull, an anatomic specimen, and a volunteer (“patient”), were registered with paired-point matching registration to their CT images [17, 18].

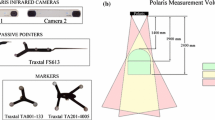
CT data for the plastic skull and the anatomic specimen were acquired with a Siemens Sensation 16 CT (Siemens, Erlangen, Germany). A Siemens Somatom Plus 4 Volume Zoom was used to acquire the imaging data for the volunteer. The imaging parameters were: for the plastic skull: convolution kernel H60s, 120 kV, 74 mA, 1 mm slice thickness; for the anatomic specimen: convolution kernel H30s, 120 kV, 175 mA, 0.6 mm slice thickness; for the volunteer: reconstruction filter H30s, 140 kV, 150 mA, 1.25 mm slice thickness. Navigation was done with open4Dnav [19], an IGSTK-based application with optical tracking (active Polaris, first generation, NDI, Ontario, Canada) [20]. MATLAB R2012a (The Mathworks, Inc., USA) was used for analyzing the data.

Isotropic [17] and anisotropic [18] image-to-patient registration was executed with MATLAB to get the transformation between image and patient space. Fiducials and targets were defined before starting the registration process for each patient.

For image-to-patient registration 3, 5, 7, and 9 fiducial points were used. For the anatomic specimen (with Ti-screws) and the volunteer (with anatomic landmarks), 10 target points were used and 11 targets were used for the plastic skull (with Ti-screws).

To verify the registration, the surgeon used a probe to point on the fiducials in patient space (FRE). This is normal clinical practice and done prior to each surgical intervention to verify navigation. If the FRE was appropriate, the TTE was determined by measuring the difference between positions as displayed by the system and “real” target points in image space. The TRE was predicted for the real target (detailed definitions are presented in “Definition of the measured errors” section).

This process was repeated 10 times for each patient and each fiducial arrangement (i.e., 3, 5, 7, and 9 fiducials), yielding 240 registration points in total for each patient, 100 targets for the anatomic specimen and the volunteer, and 110 targets for the plastic skull.

For each target in image space, the mean value of the 10 repetitions of the localization data in image space was analyzed and set as reference target points [21].

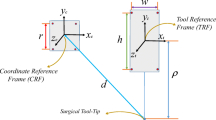
A detailed description of the experiment can be found in [16]; the setup can be seen in Fig. 1.

Fig. 1
figure 1

Experimental setup. The patient is fixed on the OR table. For all experiments the surgeon was using the same probe. The active NDI camera, the navigation system’s monitor, and the tracker unit are placed in optimal working distance. The DRF is attached near the patient

Full size image

Definition of the measured errors

Let \(x_{ij}\) and \(y_{ij}\) represent corresponding points (fiducials) in image and patient space, respectively, where \(i = 1, {\ldots }, 10\) is the number of the registration and \(j = 1, {\ldots }, {m}\) is the number of the fiducials; \({m} = 3, 5, 7, 9\).

Let \(r_{ik}\) and \(q_{ik}\) be the corresponding targets in image and patient space, respectively, where \(i = 1, {\ldots }, 10\) is the number of registration, \(k = 1, {\ldots }, n\) is the number of the target; \(n = 10\) for anatomic specimen and volunteer, and \(n = 11\) for the plastic skull.

Reference targets \(r_{k\left( m \right) } \) in image space are defined as \(r_{k\left( m \right) } =\sum _{i=1}^{10} \frac{r_{ik} }{n}\), the mean of target k over all registrations with \(m = 3, 5, 7\), and 9 fiducials, respectively. For each experiment with m fiducials, the reference targets are calculated separately.

Isotropic registration: Image fiducials were registered to patient fiducials with the transformation that minimizes

$$\begin{aligned} \mathrm{FRE}_{\mathrm{iso},i}^2 =\frac{1}{m} \sum \limits _{j=1}^m \left( {R_{\mathrm{iso},i} x_{ij} +t_{\mathrm{iso},i} -y_{ij}} \right) ^{2}. \end{aligned}$$
(1)

For registration i, the rotation matrix \(R_{\mathrm{iso},i}\), the translation \(t_{\mathrm{iso},i}\), and \({\mathrm{FRE}}_{\mathrm{iso},i}\) were saved.

The experimental TTE is the norm of the difference vectors of measured and navigated targets using

$$\begin{aligned} \mathrm{TTE}_{\mathrm{exp},i} = \parallel r_k -\left( {R_{\mathrm{iso},i} q_{jk} +t_{\mathrm{iso},i} } \right) \parallel ^{2}. \end{aligned}$$
(2)

The values of \({\mathrm{TTE}}_{\mathrm{exp},i}\) were used as the reference TRE to be compared with the TRE of the different prediction methods.

\({\mathrm{RMS(FLE}}_{i,\mathrm{img}})\) and \(\mathrm{RMS(FLE}_{i,\mathrm{pat}})\) in image and patient space, respectively, were estimated as the traces of the covariance matrix of image and patient fiducials of the i-th repetition, respectively:

$$\begin{aligned} \mathrm{RMS}\left( {\mathrm{FLE}_{i,\mathrm{img}} } \right) =\sqrt{\mathrm{trace}\left( {\mathrm{cov}\left( {x_{ij} } \right) } \right) }, \end{aligned}$$
(3)

and

$$\begin{aligned} \mathrm{RMS}\left( {\mathrm{FLE}_{i,\mathrm{pat}} } \right) =\sqrt{\mathrm{trace}\left( {\mathrm{cov}\left( {y_{ij} } \right) } \right) }. \end{aligned}$$
(4)

The total FLE for registration i, \(\mathrm{TFLE}_{i}^{2}\mathrm{= (RMS(FLE}_{i,\mathrm{img}}))^{2}+ \mathrm{(RMS(FLE}_{i,\mathrm{pat}}))^{2}\), can be treated as a single random variable [22,23,24].

The target localization error for registration i (similar to FLE) is defined as

$$\begin{aligned} \mathrm{TLE}_{i}^{2}\mathrm{= TLE}_{i,\mathrm{img}}^{2}\mathrm{\, +\, TLE}_{i,\mathrm{pat}}^{2} \end{aligned}$$
(5)

\(\mathrm{TLE}_{i,\mathrm{img}}^{2}\) and \(\mathrm{TLE}_{i,\mathrm{pat}}^{2}\) are defined as \(\mathrm{RMS}\left( {\mathrm{TLE}_{i,\mathrm{img}} } \right) =\sqrt{\mathrm{trace}\left( {\mathrm{cov}\left( {r_{ij} } \right) } \right) }\) and \(\mathrm{RMS}\left( {\mathrm{TLE}_{i,\mathrm{pat}} } \right) =\sqrt{\mathrm{trace}\left( {\mathrm{cov}\left( {q_{ij} } \right) } \right) }\), respectively. The TLE is equivalent to the FLE, but measured on targets, not on fiducials. Knowing all target positions in image and patient space allows to calculate the TLE, contrary to the definition in [25, 26] where the target positions are unknown.

Anisotropic registration considers anisotropic noise in the measurement data, image data, etc., and FRE becomes

$$\begin{aligned} \mathrm{FRE}_{\mathrm{aniso},i}^2 =\frac{1}{m}\sum \limits _{j=1}^m W_{ij} \left| {R_{\mathrm{aniso},i} x_{ij} +t_{\mathrm{aniso},i} -y_{ij} } \right| ^{2} \end{aligned}$$
(6)

has to be minimized. \(W_{ij} =V_{ij}^T \mathrm{diag}\left( {\sigma _{j1}^{-1} ,\sigma _{j2}^{-1} ,\sigma _{j3}^{-1} } \right) V_{ij}\) is the weighting matrix, where \(I=V_j^T V_j\), a 3\(\times \)3 identity matrix, and the columns of \(V_{j}\) are the principal axes of the FLE for fiducial j, and \(\sigma _{j\alpha } ,\alpha =1,2,3\), are the standard deviations of the FLE, resolved in three uncorrelated components along orthogonal principal axes [18].

TRE prediction methods

For TRE prediction 6 different estimation methods were used and are described in this section: \({\mathrm{TRE}}_{F,\mathrm{FLE}}, \mathrm{TRE}_{F,\mathrm{FRE}}, {\mathrm{TTE}}_{F,\mathrm{FLE}}, \mathrm{TTE}_{F,\mathrm{FRE}}, \mathrm{TRE}_{D}\), and \(\mathrm{TRE}_{W}\); \(<.>\) denotes the expected value.

  1. (a)

    Fitzpatrick [6] derived an expression for the expected value of the TRE which is based on the linearization of the rigid point registration problem. It is a closed-form solution to estimate the \(\mathrm{TRE}_{F}\), where FLE follows an independent and identically distributed (iid) zero-mean Gaussian distribution. The expected \({\mathrm{TRE}}_{F}\) of a target r obtained on base of the \(\mathrm{FLE}, \mathrm{TRE}_{F,\mathrm{FLE}}\), is

    $$\begin{aligned} \langle \mathrm{TRE}_{F,\mathrm{FLE}}^2 \left( r \right) \rangle =\frac{\langle \mathrm{FLE}^{2}\rangle }{N}\left( 1+\frac{1}{3} \sum \limits _{k=1}^3 \frac{d_k^2 }{f_k^2 }\right) \end{aligned}$$
    (7)

    where \(d_{k}\) is the distance of r from the principal axis k of the fiducial configuration and \(f_{k}\) is the RMS distance of the fiducials from that principal axis. For the prediction \(\mathrm{of\, TRE}_{F,\mathrm{FLE}}\) the measured \(\mathrm{TFLE}_{j}\) was used as an approximation to \(\langle \mathrm{FLE}^{2} \rangle \).

  2. (b)

    In addition, \(\mathrm{TRE}_{F,\mathrm{FRE}}\) was predicted with the expected value of \(\langle \mathrm{FLE}_{\mathrm{iso,est},j} \rangle \) estimated from \(\langle \mathrm{FRE}_{\mathrm{iso},j}\rangle \) of registration j, \(\langle \mathrm{FLE}_{\mathrm{iso,est},j}^2\rangle =\frac{m}{m-2}\langle \mathrm{FRE}_{\mathrm{iso},j}^2\rangle \) [6]; m is the number of fiducials used for registration.

  3. (c)

    The target localization error (TLE) is the error made in localizing the target (the probe is placed at target r, but the system reports target r \(^\prime \) [26]). The system makes a TLE, which is uncorrelated to TRE and so \(\langle \mathrm{TTE}_{F,x} ^{2}\rangle =\langle \mathrm{TRE}_{F,x} ^{2}\rangle +\langle \mathrm{TLE}^{2}\rangle \). TLE can be measured (see “Definition of the measured errors” section), and so the \(\mathrm{TTE}_{F,x}\) can be reported. Here \(\langle \mathrm{TRE}_{F,x}^{2}\rangle \) and \(\langle \mathrm{TTE}_{F,x}^{2}\rangle \) indicate \(\mathrm{TRE}_{F,\mathrm{FLE}}, \mathrm{TRE}_{F,\mathrm{FRE}}, \mathrm{TTE}_{F,\mathrm{FLE}}\) and \(\mathrm{TTE}_{F,\mathrm{FRE}}\), respectively.

  4. (d)

    Wiles [8] presented a closed-form solution estimation of \(\mathrm{TRE}_{W}\) similar to [6], but with anisotropic normally distributed FLE. With this approach the \(\langle \mathrm{RMS(TRE}_{W})^{2} \rangle \) and the covariance matrix \(\mathrm{of \,TRE}_{W}\) can be obtained for predicting anisotropic application accuracy.

  5. (e)

    The generalized prediction of Danilchenko [10], given as \(\langle \mathrm{TRE}_{D} \rangle \), is valid for anisotropic and isotropic FLE and arbitrary weighting of the fiducials.

Isotropic registration was used for \(\mathrm{TTE}_{\mathrm{exp}}\), \(\mathrm{TRE}_{F,x}\), and \(\mathrm{TTE}_{F,x}\); anisotropic registration was used for \(\mathrm{TTE}_{\mathrm{exp,aniso}}\), \(\mathrm{TRE}_{F,x,\mathrm{aniso}}\), \(\mathrm{TTE}_{F,x,\mathrm{aniso}}\), \(\mathrm{TRE}_{D}\), and \(\mathrm{TRE}_{W}\), with \(x = \mathrm{FLE \,or\, FRE}\). In [16] anisotropy of fiducials, measurements, and the setup was detected. Thus, it is clear that anisotropic registration had to be used for this analysis.

ULE

The user localization error (ULE) is the pure user error of placing the probe on a fiducial and has already been defined and evaluated in [16]. Two different approaches were defined: Predict the \(\mathrm{ULE}_{F}\) with \(\mathrm{TTE}_{F,\mathrm{FRE}}\) or calculate the ULE with measured errors \((\mathrm{TFLE, FLE}_{\mathrm{img}}, \mathrm{FLE}_{\mathrm{tracker}}, \mathrm{FLE}_{\mathrm{probecalib}})\):

$$\begin{aligned}&\langle \mathrm{ULE}_F^2\rangle =\frac{1}{1+\frac{1}{N}\left( {1+\frac{1}{3} \sum \nolimits _{k=1}^N \frac{d_k^2 }{f_k^2 }} \right) }\times \left[ \left\langle \mathrm{TTE}_{F,\mathrm{FRE}}^2\right\rangle .\right. \nonumber \\&\quad \quad \left. -\frac{1}{N}\left( {1+\frac{1}{3}\sum \limits _{k=1}^N \frac{d_k^2 }{f_k^2 }} \right) \left( \langle {\mathrm{FLE}_{\mathrm{tracker}}^2\rangle +\langle \mathrm{FLE}_{\mathrm{probe}_{\mathrm{calib}} }^2}\rangle \right) \right] \nonumber \\&\qquad -\langle \mathrm{FLE}_{\mathrm{img}}^2\rangle \end{aligned}$$
(8)

and

$$\begin{aligned}&\langle \mathrm{ULE}^{2}\rangle =\langle \mathrm{TFLE}^{2}\rangle -\langle \mathrm{FLE}_{\mathrm{img}}^2\rangle -\langle \mathrm{FLE}_{\mathrm{tracker}}^2\rangle \nonumber \\&\quad -\langle \mathrm{FLE}_{\mathrm{probe}_{\mathrm{calib}} }^2\rangle . \end{aligned}$$
(9)

Since measurement errors had occurred that we were not aware of in [16] (see “Data inspection and analysis” section), the results of the ULE are reported here correctly, calculated with formulae 8 and 9.

Data inspection and analysis

While assessing anisotropic registration doubts arose about the validity of the raw data; re-analysis revealed that the experimental conditions must have changed during the measuring sessions. Unfortunately this was not discovered in our previous work [16]. All patients’ data were measured relative to a DRF; thus, changes that occurred due to temporal drift can be well observed. It was detected that the raw experimental data for the anatomic specimen, registration with three fiducials, repetitions 9 and 10, were off up to 2 mm in x-, y-, and z-direction in tracker space. This is not possible when bone-anchored fiducials are used that are still rigidly in place. Obviously the anatomic specimen, the patient tracker (dynamic reference frame, DRF), or the whole setup was slightly changed unnoticed. Therefore, these two repetitions were eliminated from further analysis.

The raw data for the volunteer for registrations with 7 and 9 points were not utilizable either: Every fiducial underwent a change of up to 10 mm in x-, y-, and z-directions. As this was an investigation with a volunteer, no general anesthesia was used and the volunteer’s head was fixed to the operating table with a tape, which is a common practice in our hospital [27]. Thus, it is probable that the causes for this discrepancy were unnoticed movements of the head and/or a warming of the plastic material and a subsequent thermally induced mechanical deformation of the supporting material on the OR table. Certainly, user errors cannot be 100% excluded. Therefore, the experiments with 7 and 9 registration fiducials were eliminated from further analysis.

No problematic issues were detected for the data of the plastic skull.

All outliers that found were clearly detectable visually. These outliers were also detected by an outlier detection algorithm [28]. The algorithm found some more outliers, and clearly this is depending on the defined threshold. If one fiducial in one experiment was detected as an outlier, the whole repetition had to be removed. For the plastic skull repetitions 2, 2, 5, and 5 had to be removed for the 3, 5, 7, and 9 fiducial experiments, respectively. For the cadaver repetitions 2, 3, 1, and 5 for the 3, 5, 7, and 9 experiments, respectively, had to be removed.

For the volunteer parts of 7- and 9-point registrations had to be removed. For the 7-point registration only two repetitions and for the 9 points registration only 4 repetitions remained; thus, no statistically relevant result could be expected, and for this reason, the complete series was removed.

This generated a rather limited set of measurements, and so only the “obvious” outliers were excluded. The removal of outliers did not have significant influence on the data, see Tables 1 and 2.

In contrast to prior analysis [16], this work has used a reduced dataset without systematic errors. Therefore, a total data number of 240, 234, and 80 fiducials were available for the plastic skull, the anatomic specimen, and the volunteer, respectively.

Due to the rather small size of the dataset, a robust covariance matrix estimator for the FLE had to be used [29]; results were compared to the standardly implemented non-robust approach.

Contrary to [16] this work has used \(\mathrm{FRE}_{\mathrm{iso},i}\) (for the current experiment i) instead of the expected value of \(\langle \mathrm{FRE}_{\mathrm{iso},i}^2\rangle \) to estimate \(\langle \mathrm{FLE}_{\mathrm{iso,est},i}^2\rangle \). Moreover, the FLE of probe calibration (\(\mathrm{FLE}_{\mathrm{probe}\_\mathrm{calib}}\)) was corrected from \(0.18^{2}~\hbox {mm}^{2}\), as used earlier [16], to \(0.36^{2}~\hbox {mm}^{2}\).

Summarizing, this is expected to provide a fairly comprehensive analysis of the application accuracy in rigid-body registration for computer-assisted surgery systems.

Statistics

As from [30] the predicted TRE is influenced by the TLE, which leads to a larger (TTE) prediction error:

$$\begin{aligned} \langle \mathrm{TTE}_{F,x}^{2}\rangle = \langle \mathrm{TRE}_{F,x}^{2}\rangle + \langle \mathrm{TLE}^{2}\rangle . \end{aligned}$$
(10)

Equation (10) assumes that \(\mathrm{TRE}_{F,x}\) and TLE are uncorrelated, which is considered “likely” to be true in [30]. A significant correlation between \(\mathrm{TRE}_{F,x}\) and TLE in “real” world would suggest that \(\mathrm{TTE}_{F,x}\) as defined in (10) might not be useful for real intraoperative use/experiments. The correlation of the before-mentioned quantities was investigated with Kendall’s \(\uptau \) and Spearman’s correlation coefficient.

Normality of the distributions of measured data was statistically tested with a one-sample Kolmogorov–Smirnov test. The equality (non-equality) of the different distribution pairs was tested with a two-sample Kolmogorov–Smirnov test.

The two-sided Wilcoxon signed rank test for zero median was applied to test for statistically significant differences between predictions and measurements. The null hypothesis for this test was \(\hbox {H}_{0}\): the median of \({M} - {P} = 0\), and the alternative hypothesis was \(\hbox {H}_{1}\): the median of \({M} - {P} \ne 0\), with M = measurement and P = prediction. From a clinical perspective it is senseful to provide an upper limit for the TRE, since overestimating the uncertainty in the application accuracy provides a larger safety margin to surgeons intraoperatively. The one-sided Wilcoxon signed rank test was used to test whether the predictor overestimates the “real” measured error (with \(\hbox {H}_{0}\): the median of \({M} - {P} = 0\); \(\hbox {H}_{1}\): the median of \({M} - {P} < 0\)).

Throughout the analysis, the level of significance was 0.05.

Fig. 2
figure 2

Plastic skull. Mean TREs of anisotropic (right) and isotropic (left) registration. Three (blue dotted line), 5 (red chain line), 7 (green dashed line), and 9 (cyan solid line) fiducials were used for registration. \(\hbox {TTE}_{\mathrm{exp}}\) was measured, and the different TREs were calculated. This was repeated 10 times. The mean of the 10 repetitions was calculated. For a clear view, no standard deviation is plotted. Using more fiducials for registration a decrease in \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{D}\), and \(\hbox {TRE}_{W}\) can be observed

Full size image

Numerical simulation of TRE prediction and measurements

A numerical simulation of the experiment might give information concerning eventual correlation of TRE and TLE random variables and how localization errors affect target errors. Two different experiments were made: an independent (unpaired) and a dependent (paired) one: Predicting the TRE with FLE led to an independent experiment, because all repetitions were used for the estimation of FLE (compared to the real experiments). On the other hand, the experiment is dependent if the FRE was used for the prediction of the TRE, because the very same samples were used both for measurement and for prediction.

The following simulation was repeated 100,000 times with 3, 5, 7, and 9 fiducials, respectively:

  1. (a)

    Creation of registration fiducials: Draw N 3-dimensional random patient fiducial points \(X_{i}\), \(i = 1, {\ldots }, N\), in patient space inside a cube with an edge length of 200 mm. These are the true patient fiducials. \(N = 3, 5, 7\), or 9.

  2. (b)

    Create a random rotation matrix \(R_{\mathrm{rand}}\) and apply to the \(X_{i}\) to yield N true image points \(Y_{i}\).

  3. (c)

    Select a specific localization error in patient and image space, \(\mathrm{FLE}_{\mathrm{sim,pat}} = 1/3~\hbox {mm}\) and \(\mathrm{FLE}_{\mathrm{sim,img}} = 0.0001~\hbox {mm}\), combined to \(\mathrm{FLE}_{\mathrm{sim}}^{2} = \mathrm{FLE}_{\mathrm{sim,img}}^{2} + \mathrm{FLE}_{\mathrm{sim,pat}}^{2}\).

  4. (d)

    Perturb \(X_{i}\) with \(\varDelta x\), a zero-mean Gaussian noise with standard deviation \(\mathrm{FLE}_{\mathrm{sim,pat}}\) in all directions and \(Y_{i}\) with \(\varDelta y\), a zero-mean Gaussian noise with standard deviation \(\mathrm{FLE}_{\mathrm{sim,img}}\) in all directions, so that \(X'_{i} = X_{i} + \varDelta x\), and \(Y'_{i} = Y_{i} + \varDelta y\).

  5. (e)

    Register the \(X'_{i}\) to \(Y'_{i}\) to get rotation \(R_{\mathrm{sim}}\), translation \(t_{\mathrm{sim}}\), and \(\mathrm{FRE}_{\mathrm{sim}}\).

  6. (f)

    Create one “true” random target patient point r inside the cube and transform it to image space with \(R_{\mathrm{rand}} * r = q\).

  7. (g)

    Generate M perturbed random target points \(r_{j}\) with mean(\(r_{j})=r\) and \(\hbox {std}(r_{j}) = \mathrm{FLE}_{\mathrm{sim,pat}}\), \(j = 1,{\ldots }, M; M = 100,000\). Transform \(r_{j}\) into image space (\(q_{j} = R_{\mathrm{sim}} * r_{j} + t_{\mathrm{sim}}\)) and calculate the measured TRE for the M points, \(\mathrm{TTE}_{sim}(q_{j}) = \Vert q - q_{i}\Vert \).

  8. (h)

    Calculate \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\) for q and \(q_{i}\) (see Sect. 2.3b).

For the independent experiment, all steps (except h) are repeated again and \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FLE}}\) is calculated (see Sect. 2.3a).

The simulation was repeated 10 times to calculate mean and standard deviation of all errors.

The distributions of \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FLE}}\), \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\), and \(\mathrm{TTE}_{\mathrm{sim}}\) were analyzed. Correlations between the errors were tested with Pearson’s correlation coefficient. Equality or difference of prediction and measurement was tested using a Wilcoxon signed rank test (in case of paired samples) and a Wilcoxon rank sum test (in case of unpaired samples). Power and effect sizes of the experiments were evaluated.

Results

The results for all patients with isotropic registration and prediction are presented on the left half of Figs. 2, 3, 4, 5, 6, and 7. The right half of Figs. 2, 3, 4, 5, 6, and 7 shows the results for anisotropic registration and predictions. For each target the mean measured and mean predicted error is visualized for the registrations with 3, 5, 7, and 9 fiducials. Tables 1, 2, 3, 4, 5, and 6 show the measured and predicted TREs and TTEs for all objects studied.

Fig. 3
figure 3

Plastic skull. Mean TRE results of 3, 5, 7, and 9 fiducial arrangements (from top to bottom) and 10 repetitions. Standard deviation of \(\hbox {TTE}_{\mathrm{exp}}\) (red solid line) is shown; it can be observed that most of the predicted TREs are lying within \(\hbox {TTE}_{\mathrm{exp}}\) ± standard deviation. Isotropic registration on the left, anisotropic registration on the right side. Differences between anisotropic and isotropic registration can be observed, but also the similarity of predictions and measurements

Full size image
Fig. 4
figure 4

Anatomic specimen. Mean TREs of anisotropic (right) and isotropic (left) registration. Three (blue dotted line), 5 (red chain line), 7 (green dashed line), and 9 (cyan solid line) fiducials were used for registration. \(\hbox {TTE}_{\mathrm{exp}}\) was measured, and the different TREs were calculated. This was repeated 10 times. The mean of the 10 repetitions was calculated. For a clear view, no standard deviation is plotted. Using more fiducials for registration a decrease in \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{D}\), and \(\hbox {TRE}_{W}\) can be observed. The predictions lead to larger errors than the measurements (different to the plastic skull)

Full size image
Fig. 5
figure 5

Anatomic specimen. Mean TRE results of 10 repetitions of 3, 5, 7, and 9 fiducial arrangements (from top to bottom). Standard deviation of \(\hbox {TTE}_{\mathrm{exp}}\) (red solid line) is shown; it can be observed that most of the predicted TREs are lying within \(\hbox {TTE}_{\mathrm{exp}}\) ± standard deviation. Isotropic registration on the left, anisotropic registration on the right side. Differences between anisotropic and isotropic registration can be observed, but also the similarity of predictions and measurements

Full size image
Fig. 6
figure 6

Volunteer. Mean TREs of anisotropic (right) and isotropic (left) registration. Three (blue dotted line) and 5 (red chain line) fiducials were used for registration. \(\hbox {TTE}_{\mathrm{exp}}\) was measured, and the different TREs were calculated. This was repeated 10 times. The mean of the 10 repetitions was calculated. For a clear view, no standard deviation is plotted. With a 5-point registration, the target error is smaller than with a 3 points registration for \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{F,\mathrm{FLE}}\), \(\hbox {TRE}_{D}\), and \(\hbox {TRE}_{W}\). The predictions lead to larger errors than the measurements with isotropic registration, different to anisotropic registration

Full size image
Fig. 7
figure 7

Volunteer. Mean TRE results of 10 repetitions of the 3 and 5 fiducial arrangements (from top to bottom). Isotropic registration on the left, anisotropic registration on the right side. Standard deviation of \(\hbox {TTE}_{\mathrm{exp}}\) (red solid line) is shown; it can be observed that only \(\hbox {TRE}_{F,\mathrm{FLE,iso}}\) is lying within \(\hbox {TTE}_{\mathrm{exp}}\) ± standard deviation when using isotropic registration. For anisotropic registration \(\hbox {TTE}_{\mathrm{exp, aniso}}\) is much higher than all the predicted TREs

Full size image

A robust estimation of the covariance matrix led to smaller TREs (Tables 4, 6). If the outliers are not included, and a robust estimation is used, the TRE gets larger again (Tables 1, 2). For the anatomic specimen robust approach gives an overall improvement, where more predictions equal the measurements in terms of statistical equivalence (see Table 8). We focus on the results of non-robust covariance matrix estimations. The detailed results with robust estimation can be seen in the mentioned tables. Table 10 shows \(\mathrm{ULE}_{\mathrm{exp}}\) and \(\mathrm{ULE}_{F}\) as determined from the data. Table 11 shows the FLE as determined over all registrations and fiducials. Tables 7, 8, and 9 give the total number of targets, where equality or overestimation of the prediction can be statistically confirmed for all patients. The results of the numerical simulation are reported in Table 12.

Detailed remarks on the data:

Plastic skull The lowest application error, \(\mathrm{TTE}_{\mathrm{exp}}\), could be achieved with a registration with 9 fiducials; with anisotropic registration \(\mathrm{TTE}_{\mathrm{exp}}\) was improving.

Table 7 shows good correspondence of experiments and predictions. Regarding isotropic registration, \(\hbox {TRE}_{F,\mathrm{FLE}}\) and \(\hbox {TTE}_{F,\mathrm{FRE}}\) gave the most similar results for \(\mathrm{TTE}_{\mathrm{exp}}\) for 3 registration points. (with the statistical power \(\le \)0.61 for 3-fiducial registration, \(\le \)0.94 for 5 fiducials, \(\le \)0.24 for 7 fiducials, and \(\le \)0.00001 for 9 fiducials for \(\mathrm{TRE}_{F,\mathrm{FLE}}\)). All targets were overestimated with \(\mathrm{TTE}_{F,\mathrm{FRE}}\) using 5 and 7 registration points. Regarding anisotropic registration \(\mathrm{TRE}_{F,\mathrm{FLE,aniso}}\) and \(\mathrm{TRE}_{W}\) were predicting \(\mathrm{TTE}_{\mathrm{exp,aniso}}\) in about 70%. \(\mathrm{TTE}_{F,\mathrm{FRE,aniso}}\) and \(\mathrm{TRE}_{F,\mathrm{FRE,aniso}}\) were overestimating \(\mathrm{TTE}_{\mathrm{exp}}\) for all 11 targets in all experiments.

Anatomic specimen Predictions of target errors for different registration alternatives overestimated the measurements; this can clearly be seen in Figs. 4 and 5.

In case of isotropic registration \(\mathrm{TRE}_{F,\mathrm{FLE}}\) and \({ TRE}_{F,\mathrm{FRE}}\) were predicting \(\mathrm{TTE}_{\mathrm{exp}}\) almost always (statistical power \(\le \)0.99 for 3-fiducial registration, \(\le \)1 for 5 fiducials, \(\le \)0.98 for 7 fiducials, and \(\le \)0.99 for 9 fiducials for \(\mathrm{TRE}_{F,\mathrm{FLE}})\). \(\mathrm{TTE}_{F,\mathrm{FRE}}\) was overestimating \(\mathrm{TTE}_{\mathrm{exp}}\) for most of the targets.

In the anisotropic case, for \(\mathrm{TRE}_{W}\) and \(\mathrm{TRE}_{F,\mathrm{FLE,aniso}}\) equality to \(\mathrm{TTE}_{\mathrm{exp,aniso}}\) could be confirmed statistically in 82% of the targets. For all targets \(\mathrm{TRE}_{F,\mathrm{FRE,aniso}}\) overestimated \(\mathrm{TTE}_{\mathrm{exp,aniso}}\).

The results for the volunteer (Figs. 6, 7) show that isotropic \(\mathrm{TRE}_{F,\mathrm{FLE}}\) was the best prediction method for \(\mathrm{TTE}_{\mathrm{exp}}\); most overestimations were given by \(\mathrm{TRE}_{F,\mathrm{FRE}}\) and \(\mathrm{TTE}_{F,\mathrm{FRE}}\). The statistical power for \(\mathrm{TRE}_{F,\mathrm{FLE}}\) is \(\le \)0.91 for the 3-fiducial registration and \(\le \)0.99 for the 5-fiducial registration.

With anisotropic registration \(\mathrm{TRE}_{F,\mathrm{FRE,aniso}}\) was equal to \(\mathrm{TTE}_{\mathrm{exp,aniso}}\) for 8 out of 10 targets, with 3 registration points. \(\mathrm{TTE}_{F,\mathrm{FRE,aniso}}\) overestimated \(\mathrm{TTE}_{\mathrm{exp,aniso}}\) with 3 fiducials only; using 5 fiducials no prediction method gave satisfying results.

The correlation between \(\mathrm{TRE}_{F,\mathrm{FLE}}\) and TLE was always larger than between \(\mathrm{TRE}_{F,\mathrm{FRE}}\) and TLE (Table 13), except in the case of the volunteer, where the correlation between \(\mathrm{TRE}_{F,\mathrm{FRE}}\) and TLE reached 0.47.

Almost all target errors, measured and predicted, were not normally distributed.

The results of \(\mathrm{ULE}_{F}\) and \(\mathrm{ULE}_{\mathrm{exp}}\) are similar to each other for the anatomic specimen, but not for the plastic skull and the volunteer. The plastic skull with Ti-screws had the smallest ULE (\(\mathrm{ULE}_{\mathrm{exp}} = 0.4~\hbox {mm}\)), while the volunteer, using anatomic landmarks only, had the largest ULE (\(\mathrm{ULE}_{\mathrm{exp}} = 1.6~\hbox {mm}\)).

As a result of the numerical simulation it can be seen that the mean of the measured \(\mathrm{TTE}_{\mathrm{sim}}\) is always similar to the mean of the predicted \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\); \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FLE}}\) is the largest error (Table 12). The smallest measured and predicted errors could be achieved using 9 fiducials, which is in agreement with earlier experiments and theory. The mean of \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\) of all perturbed targets equals \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\) on the true target (this is also valid for \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FLE}}\)).

No correlation could be found between \(\mathrm{FRE}_{\mathrm{sim}}\) and \(\mathrm{TRE}_{{rm sim},F,\mathrm{FLE}}\) and between \(\mathrm{TTE}_{\mathrm{sim}}\) and \({ TRE}_{\mathrm{sim},F,\mathrm{FLE}}\) and \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\), respectively (the mean correlation coefficient is always smaller ±0.02 ±0.00). The correlation of \(\mathrm{TRE}_{\mathrm{sim},F,\mathrm{FRE}}\), and \(\mathrm{FRE}_{\mathrm{sim}}\) was always 1.

Visual inspection showed that none of the errors were normally distributed. Statistical testing with the Kolmogorov–Smirnov method, the \(\hbox {H}_{0}\) hypothesis (that the error is normally distributed) had to be rejected for all errors at the 5% significance level. Since the measured errors are Euclidean distances of normally distributed points, their distribution is expected to resemble the Maxwell distribution [31, 32]. Figure 8, a plot of the pdf of the errors, shows this. The power of the numerical simulation is 1, with a small effect size. The difference of the distributions of measured and predicted errors could always be statistically confirmed. The distributions of the independent TREs were the same as in the dependent situation.

Discussion

For rigid-body registration in clinical navigation, a complete and detailed analysis of anisotropic and isotropic prediction methods for TRE is presented. Two major groups were distinguished based on isotropy and anisotropy. For the isotropic case, isotropic registration and isotropic prediction methods were used to measure and predict the TRE. The anisotropic case handled anisotropic registration with anisotropic prediction methods; the most widely used prediction method (\(\mathrm{TRE}_{F,x,\mathrm{aniso}}\)) was added, though it is, strictly speaking, defined for isotropic FLE only [6].

Table 1 Isotropic registration
Full size table
Table 2 Anisotropic registration
Full size table
Table 3 Isotropic registration
Full size table
Table 4 Isotropic registration
Full size table
Table 5 Anisotropic registration
Full size table
Table 6 Anisotropic registration
Full size table
Table 7 Results of the statistical tests for the plastic skull
Full size table
Table 8 Results of the statistical testing for the anatomic specimen
Full size table
Table 9 Results of the statistical testing for the volunteer
Full size table
Table 10 Mean values of the ULEs of all patients, calculated with Eqs. (8) and (9)
Full size table
Table 11 Experimental fiducial localization errors
Full size table
Table 12 Results of an example of a numerical simulation
Full size table
Table 13 Mean experimental correlation coefficients
Full size table
Fig. 8
figure 8

Example of a pdf of the measured \(\hbox {TTE}_{\mathrm{sim}}\) (left) and the predicted \(\hbox {TRE}_{F,\mathrm{FRE}}\) (right) in a numerical simulation. A 3 points registration was used to calculate 100,000 TTEs and TREs. \(\hbox {TTE}_{\mathrm{sim}} = 2.43 \pm 1.63~\hbox {mm}\), \(\hbox {TRE}_{F,\mathrm{FRE}} = 2.70 \pm 1.13~\hbox {mm}\). The difference between the two functions can clearly be seen and is statistically significant. The Gamma distribution and the Nakagami distribution are the best fits for \(\hbox {TTE}_{\mathrm{sim}}\) and \(\hbox {TRE}_{F,\mathrm{FRE}}\), respectively, for this experiment

Full size image

The prediction methods studied gave a good estimation of the application error in the surgical environment for the plastic skull and the anatomic specimen. A two-sided test was used to statistically compare predicted and measured target errors. The one-sided test might be a better approach for predicting surgically relevant application accuracy (TRE), because predictions should indicate a lower limit for the TRE on a specific target, rather than underestimate the real error. Underestimations can be very critical for patients in a real intervention. For most of the targets, however, a good estimation or overestimation of the TRE was found; equality or that the prediction was an upper limit can be statistically confirmed.

Comparing true and reference targets (compared to [16]) showed that better agreement of measured and predicted errors could be achieved if the mean of the targets of all repetitions was used for each experiment, because eventual biases were eliminated [21]. As a result, the TTEs were smaller and prediction approached the measured values.

Graphically it could be observed that for all patients the errors of measurements and predictions were getting smaller, when more fiducials were used for registration, as expected (Figs. 2, 4, 6). Using 5 fiducials or more leads to very similar results and shows that there is no need for using a large number of fiducials to improve accuracy of the navigation, as already investigated by many authors, e.g., [33]. An important result is that predictions were approaching measurements already when 3 or 5 fiducials were used for registration. Using 7 or 9 fiducials for registration TTE and TRE did not improve much, but less predicted TREs were similar to measurements.

Generally, the trend of predictions was always similar to measurements. Most of the predicted results were inside the measured TTE ± one standard deviation.

Usually \(\mathrm{TTE}_{F,\mathrm{FRE}}\) was overestimating \(\mathrm{TTE}_{\mathrm{exp}}\), but the overestimation was sometimes too large to be relevant (see Tables 7, 8, 9).

The best estimator for \(\mathrm{TTE}_{\mathrm{exp}}\) was \(\mathrm{TRE}_{F,\mathrm{FLE}}\); it predicted \(\mathrm{TTE}_{\mathrm{exp}}\) in 56.8, 72.5, and 45% of all targets of the plastic skull, the anatomic specimen, and the volunteer, respectively (the exact numbers of targets are shown in Tables 7, 8, 9).

In case of anisotropy, both \(\mathrm{TRE}_{F,\mathrm{FLE,aniso}}\) and \(\mathrm{TRE}_{W}\) predicted 68.2 and 75% of all targets for the plastic skull and the anatomic specimen, respectively. For the volunteer \(\mathrm{TTE}_{\mathrm{exp}}\) could be predicted with \(\mathrm{TRE}_{F,\mathrm{FRE}}\) in 40% of all targets (the exact numbers of targets are shown in Tables 7, 8, 9).

It has to be mentioned that all prediction methods are grounded on the same theory and the predicted TREs (all but the \(\mathrm{TTE}_{F,x})\) led to very similar results. This can be clearly seen in all figures and tables. However, the results of statistical testing showed that for these particular experiment settings different prediction methods did not lead to equal results; the number of targets where prediction was equal to measurement is different for all methods.

These findings confirm the importance of estimating FLE for the predictions; this was possible since the used navigation system provides access to all data. In a real surgical setup, it is difficult to estimate the FLE at the patient. It is always depending on how experienced the surgeon is with navigation, if the fiducials are in regions difficult to reach or if the probe at certain fiducials can be detected by the tracker.

\(\mathrm{TTE}_{\mathrm{exp}}\) is submillimetric for plastic skull and anatomic specimen. For the volunteer a \(\mathrm{TTE}_{\mathrm{exp}} = 2.3~\hbox {mm}\) is in a clinically acceptable range, with an \(\mathrm{ULE}_{\mathrm{exp}} = 1.61~\hbox {mm}\) due to anatomic landmarks only. The difference in using screws and anatomic landmarks can be observed well. Screws lead to smaller errors due to the “exact” fiducial that can be located accurately, whereas locating anatomic landmarks accurately is difficult and leads to larger user errors.

In case of the real experiments medium correlation [34] could be found between \(\mathrm{TRE}_{F,\mathrm{FLE}} \text { and } \mathrm{TLE}\) and between \(\mathrm{TRE}_{F,\mathrm{FRE}}\) and TLE (Table 13). Concerning this correlation considerable care must be taken using \(\mathrm{TTE}_{F,x}\), which can only be defined as is, if no correlation of TRE and TLE occurs. No correlations could be found for the results of numerical simulation, as required for the theoretical approach of TTE.

It could be observed that experiments with the navigation system and its simulation were leading to different results. A numerical simulation might be a good proof for theory, but it clearly differs from experiments in a real surgical situation. In reality, more complex error sources, like bias, non-normality, and temporal variations of distributions, influence the experiments and make them difficult to generalize or predict.

Although the sample size of the real experiments is relatively small, especially for the volunteer, the results are providing a good insight into the possibilities of prediction methods for the TRE. The statistical power is large compared to the sample size; this is because the difference between prediction and measurement can be clearly seen for a lot of targets. Thus, the overestimation could be confirmed statistically with a one-sided test with a small alpha value. When the difference between the means of measurement and prediction was small, the power was getting smaller as well, especially when no overestimation of the measurement could be provided. For the numerical experiment the power was always 1 due to the very large sample size. Decreasing the sample size led to a smaller power also for the numerical simulations, as can be expected.

Due to the small sample size using a robust estimate for the covariance matrix of FLE is suggested, because the covariance matrix is sensitive to outliers. With a robust estimation \(\mathrm{TRE}_{W}\) and \(\mathrm{TRE}_{D}\) were changing and could predict more TTEs as with a non-robust calculation. Especially for the anatomic specimen results improved, the prediction got more “accurate.” Though the overall means did not change a lot, the equality of measurement and prediction could be confirmed more often when a robust method was used, and less overestimations occurred (see Tables 1, 2). For the other two patients no remarkable changes could be observed (see Tables 4, 6).

Taking into consideration that more fiducials were outliers and thus less registrations could be used for calculation, we had less variance of the experiments. This makes it more difficult for the prediction to be within the standard deviation of the experimental results.

The analysis of results is hardly affected whether outliers are removed or not. However, care should be taken when outliers are removed. For the experiments the FLE and TRE values decreased if the outliers were removed, but the whole measurement process itself is characterized as is and is not affected by this.

Only those points were excluded, where an obvious mistake in the measurement occurred, such that it was easy to confirm visually the impossibility to reach the position under consideration in the experimental setup. All other outliers found by the algorithm were a result of, i.e., systematic, temporally varying bias and non-static bias which are inherent to the measurement process (cf. “Data inspection and analysis” section). A detailed investigation of the effect of bias was already done in [35].

Registration had no influence on FLE; thus, there was no difference between \(\mathrm{TRE}_{F,\mathrm{FLE}}\) and \(\mathrm{TRE}_{F,\mathrm{FLE,aniso}}\) and furthermore between \(\mathrm{TTE}_{F,\mathrm{FLE}}\) and \(\mathrm{TTE}_{F,\mathrm{FLE,aniso}}\) (c.f. Tables 3, 5).

Surface registration might benefit of these results as well. Though the registration is different, it uses point correspondences too [4]. It is clear that only tracker and calibration error influence the FLE in surface registration; ULE and \(\mathrm{FLE}_{\mathrm{image}}\) are negligible. As we observed in our experiments eventual anisotropy did not influence the prediction much, Fitzpatrick’s TRE is an adequate model to estimate the TRE in a surgical setting.

Previous numerical experiments were not analyzing the distributions of the predicted and measured errors ([6, 8,9,10,11]). Detailed analysis of the numerical simulation showed that prediction and measurement were coming from different distributions (an example is shown in Fig. 8). Thus, it is clear that the results of prediction and measurement could not be equal, both in real experiments and in simulation In general, the distribution of a measurement of a vector length is similar to a Maxwell distribution [32]. In general, it is very challenging to know and to characterize the distribution of the experimental data, specifically for small sample sizes and when data acquisition is a lengthy and labor-intensive undertaking. For one repetition of the numerical experiment, the difference between the distributions of measurement and prediction could always be well observed and tested (Fig. 8). The means and standard deviations of measured and predicted TREs would suggest that it is possible to predict the measured TTE, because they were similar for prediction and measurement. However, predictions did not result in an upper limit. Whether overestimation of the measurement can be achieved with \(\mathrm{TRE}_{F,\mathrm{FLE}}\) is dependent on the FLE defined for the simulation. This indicates that the FLE is the important factor for the prediction and should be estimated well prior to the experiments. In the independent case, the difference between measurement and prediction was getting larger, because different fiducials and targets were used. Like real experiments, where measurement, tracking, and user errors influenced the prediction, numerical experiments showed that an improvement in the simplest TRE prediction (\(\mathrm{TRE}_{F,\mathrm{FRE}}\)) might not be necessary.

Conclusion

Experiments with a plastic skull, an anatomic specimen, and a volunteer were analyzed to predict and measure intraoperative application errors made before and during surgery. Isotropic and anisotropic registration and prediction methods were used, and prediction of the TRE was compared to the measured TRE. Best results for an upper limit of TRE were provided by \(\mathrm{TTE}_{F,x}\); the most similar results were achieved with \(\mathrm{TRE}_{F,\mathrm{FLE}}\) and \(\mathrm{TRE}_{F,\mathrm{FRE}}\). According to our experiments, using anisotropic registration and/or prediction methods did not significantly improve the results of the predictions. The smallest ULE was found for the plastic skull with Ti-screws only; the largest ULE was found for the volunteer with anatomic landmarks only.

To our knowledge, this is the first investigation where the accuracy of navigation of simulated clinical experiments is compared to commonly used prediction methods, using anisotropic and isotropic registrations. A detailed error analysis of three patients in an experimental clinical setup was conducted, possibly due to a detailed data collection, that demonstrated the usefulness of an open navigation system.