1 Introduction

Cholera is a disease spread by Vibrio cholerae, causing diarrhea and severe dehydration in about one out of 20 patients. Cholera can be endemic, leading to seasonal outbreaks, or epidemic. According to the World Health Organization (WHO), cholera incidence has increased globally since 2005 with in 2012 48 % of cholera cases occurring in Africa (WHO 2014).

Cholera infection can be caused by ingestion of food or water contaminated by V. cholerae and has two distinct life-cycles, one in the environment and another in humans (Harris et al. 2012). The pathogen occurs naturally in coastal waters, preferring brackish water and can live in association with zooplankton and shellfish (Harris et al. 2012; Sedas 2007). The intake and passage of V. cholerae through the human body results in conversion of the pathogen to a hyperinfectious state. When shed via faecal excretion of infected individuals, hyperinfectious bacteria can be re-introduced into the environment and pose a severe risk to other individuals as the infectious dose is 10–100 times lower compared to natural, non-human shed low-infectious organisms (Harris et al. 2012). When present in the environment either as a natural pathogen or in hyperinfectious state, bacteria can be transported via rivers, leading to further propagation of the disease to previously uninfected areas potentially causing new exposure.

Health risks also depends on human factors, like the cultural and socio-economic environment (Tamerius et al. 2007). When a community has access to safe water and does not use surface water in their daily routines (drinking water, sanitation, hand-washing and food preparation), chances of infection are minimal (Penrose et al. 2010). According to a study by Devas and Korboe (2000), only 30 % of Kumasi households had satisfactory sanitation arrangements in their own home, 40 % depended on public toilets and 24 % of the households were using buckets. With public toilets often having waiting queues, people (especially children) relieve themselves on open dumpsites. Besides problems with sanitation, Kumasi also struggled with water supplies. Although most households have access to tap water, these are unreliable (Devas and Korboe 2000).

In recent research on the 2005 cholera outbreak in Kumasi, it has been suggested that dumpsites played a role in the spread of hyperinfectious V. cholerae. Due to fast urbanisation and growing population, Kumasi Waste Management Department (WMD) in 1999 collected only 40 % of the total waste (Post 1999) leading to many open refuse dumps. Spatial dependency of cholera infections on the proximity to and density of refuse dumps was shown by Osei et al. (2010). This implies that runoff from dump sites could carry faecal materials to local rivers, creating a pathway for faecal contamination of surface water. A strong increase in the number of communities reporting cholera cases during/after rainfall periods underlines this hypothesis. A study from Obiri-Danso et al. (2005) revealed high bacteria counts (faecal coliforms) in the Subin river running through Kumasi in 2000–2001 during the rainy season. During periods of rainfall, Kumasi suffers from sporadic water shortage, leading to a higher use of river water. The booster effect of rainfall on cholera outbreaks has been reported for a number of other countries like Haiti and Guinea-Bissau (Gaudart et al. 2013; Luquero et al. 2011). Effect of extreme precipitation on waterborne diseases in the United States was reported by Curriero et al. (2001).

The link between disease and inproper solid waste disposal has gained more attention lately (Ayomoh et al. 2008; Boadi and Kuitunen 2005; McMichael 2000; Obiri-Danso et al. 2005). Worldwide, the problem of proper solid waste disposal increased because of growing urbanization, increase in the amount of solid waste produced per household, and lack of proper waste collection, dumpsite planning and treatment methods. In Ghana, Anaman and Nyadzi (2015) and Bagah et al. (2015) studied the improper disposal of solid waste showing the magnitude of this problem in Accra, and linking this to a cholera outbreak. Rego et al. (2005) found a link between diarrhoea and garbage disposal in Brazil. Abul (2010) related cholera to solid waste disposal in Swaziland for homes located within a 200 m distance of dumpsites.

Modelling provides a good means of gaining deeper understanding of the process that caused the 2005 cholera outbreak, as it can provide more insight in disease diffusion patterns (Meade and Emch 2010; Mikler et al. 2007). Most cholera models fall back on a model developed by Codeço (2001) which was extended to include a transient hyperinfectious state of the pathogen by Hartley et al. (2006). Several geographically explicit cholera models have been developed including both natural and hyperinfectious cholera transmission including transportation via river networks (Bertuzzo et al. 2008, 2009; Mari et al. 2012). Most of these models focus on spread of cholera between villages and cities linked by a river, coupling a local disease model with a transport model in order to model cholera diffusion. These models provide excellent tools to study cholera diffusion patterns at a larger scale, but are less suitable for micro-scale modelling. Although these models simulate the transport of the pathogen via the river pathway, they do not include the route of V. cholerae to the river. This is not easily incorporated into the network structure as there is no permanent flow of water, but flow only occurs after heavy rainfall.

Investigating the potential transport route of V. cholerae from dumpsite to river is interesting, because interventions can easily be executed (e.g. relocation of dumpsites) when the contribution of runoff as a transport mechanism can be proven. Agent-based models (ABMs) are particularly suitable to perform geographically explicit micro-simulations, which include both human behaviour as well as environmental aspects. They have proven to be particularly useful when assessing control measures (Dommar et al. 2014). A strategy called pattern-oriented modelling (POM) which attempts to replicate multiple spatial and non-spatial patterns observed in the real system is often applied for ABMs (Grimm et al. 2005).

We therefore propose an ABM including a disease sub-model and a hydrological sub-model to perform micro-scale simulations to determine if open refuse dumps could have played a role in cholera diffusion during the 2005 cholera outbreak in Kumasi, Ghana. This article is structured as follows: Sect. 2 contains the conceptual design of the ABM, Sect. 3 describes the experiments conducted to test the hypothesis of runoff from dumpsites causing cholera diffusion, followed by the discussion (Sect. 4) and the conclusions and recommendations (Sect. 5).

2 Conceptual model

The ABM will be described using the standard overview, design concepts and details (ODD) protocol for ABMs (Grimm et al. 2010; Polhill et al. 2008). In this structure, the “Overview” part (2.1) will discuss the purpose of the model (2.1.1), the most important components (2.1.2) and the main processes and their scheduling (2.1.3). The “Design Concepts” part (2.2) reflects on the design concepts underlying the ABM. In the “Details” part of the protocol (2.3), the three steps leading towards the implementation are discussed, starting with the initialization (2.3.1), input data needed for the model (2.3.2) and the sub-models (2.3.3).

2.1 Overview

2.1.1 Purpose

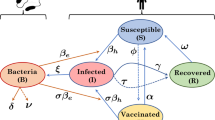
In order to test the hypothesis of cholera diffusion via runoff from dumpsites for the urban area of Kumasi we developed a model that allows us to study diffusion and persistence by means of two mechanisms: non-hyperinfectious V. cholerae transmission (environment to human, EH) and hyperinfectious V. cholerae transmission via runoff from dumpsites (human to environment to human, HEH). We assume that non-hyperinfectious bacteria are already present in the environment at the beginning of the simulation. When faecal waste from infected individuals is dumped on open refuse dumps, rain can carry these bacteria from the dumpsites to the river, temporarily infecting this river with hyperinfectious bacteria. When exposed to this water, this can lead to new (HEH) infections (see Fig. 1). When we refer to HEH transmission henceforth, this automatically includes EH transmission.

Fig. 1
figure 1

Overview of the processes included in the model

Full size image

The model builds onto existing non-spatial mathematical models for cholera dynamics that model environmental reservoirs of V. cholerae (Capasso and Paveri-Fontana 1979; Codeço 2001). However, where they model a concentration of V. cholerae in water based on the number of infected individuals and the time that V. cholerae remains infectious, we model the infectiousness of the water based on the number of disposals of faecal waste on dumpsites and the time the dumpsite remains infectious. Modelling the exact concentration would require knowledge about the exact number of bacteria and volume of water, at any location and every moment in time for the study area. With the available data this is not possible.

The aim of this research is not to fully describe the 2005 cholera outbreak in Kumasi but to determine if, based on spatial–temporal patterns, the importance of the runoff from the dumpsites in the diffusion of cholera can be confirmed. The model is fully geographically explicit, using actual locations of buildings, dumpsites etc. and recorded rainfall.

2.1.2 Entities, state variables and scales

Agent-based simulation models are built upon the concept of agents (entities) that are located within an environment, and interact with each other as well as with the environment. Agents can represent both human beings as well as more abstract phenomena like organisations and natural features. By definition, agents are heterogeneous, differentiated by their variables.

The cholera model contains three types of agents: households, individuals and rain particles (Table 1). Households are collections of individuals, however, households also have specific variables and behaviour. Examples of variables that belong to a household are income level, access to tap water and house location.

Table 1 Overview of entities included in the model
Full size table

Individuals are members of a household and inherit the properties from the households, but also have a number of personal characteristics like age and gender. Important state variable is the health status of the individual—susceptible, infected or recovered.

Rain particles are considered as agents, as they have the behaviour to move over the surface to the surface water. They can become infected (carry V. Cholerae) when their pattern of flow runs via an infected dumpsite. Examples of rain particle characteristics are the volume and travel time. The state variable of the rain particle is the infection level.

In the simulation, agents interact with a number of environments. The rain particle movement is based on a digital elevation model (DEM) for which a flow direction and flow accumulation environment are determined. These environments are static for the duration of the simulation, and are all raster layers.

Besides the environments used in the hydrological sub-model, there are two environments related to the household and individual agents: dumpsites and houses. Dumpsites represent actual locations of open refuse dumps and have a dumpsite-infection-level as their state variable. This variable is dynamic during the simulation, as dumpsites can become infected after dumping of infected waste. Dumpsite infection will disappear over time due to loss of hyperinfectiousness of V. cholera when no new re-infection occurs. Houses are used to locate the households.

All spatial layers have a resolution of 30 by 30 m. The model runs for 90 days (duration of the cholera outbreak in Kumasi), divided in time steps of 1 h. This temporal resolution is adequate to represent the flow of water over the DEM and allows for scheduling several human activities in a sequential order.

2.1.3 Process overview and scheduling

The model contains the following processes: flow of rain particles (over the DEM to the river), households fetching water and the households dumping faecal materials on the dumpsites.

The flow of rain particles over the surface will be described in detail in the section on the hydrological sub-model (2.3.3). Rainfall triggers the flow process. Rain particles can get infected by running over an infected dumpsite. Non-infected rain particles are removed from further simulation to save computation time. When reaching the river this will lead to hyperinfectious bacteria present in the river which after exposure (households fetch contaminated water) can lead to infection.

Use of water is determined by two household variables: access to tap water and income level. Households with access to tap water will use this water for their daily activities and this water is assumed to be safe for consumption. In case a household has no access to tap water, income level will determine if the household will buy safe water or use river water. This specific group of households will fetch water at the beginning of every new day. River water is collected by the household at the river point closest to the house and all individuals belonging to this household will consume this water. River water can be either infected via HEH or EH. Depending on the hygiene level of the household, the infected water can be treated (cooked) or not. Consumption of infected water can lead to infection.

All households that have infected individuals will dump waste on the nearest dumpsite. Dumpsites have an infection level that is determined by the number of infected households dumping on this site. Dumpsites become infected, and able to infect runoff, when the dumpsite infection level exceeds a threshold value.

Activities are scheduled in the following order: flow of rain particles, fetch water, dump waste. Flow of water occurs in every time step, fetching water and dumping waste only once a day. On the days it is raining, the rain falls at the beginning of the day.

2.2 Design concepts

2.2.1 Emergence

The route of cholera diffusion via runoff from dumpsites into the river can lead to a fast spread of infection to new communities downstream. This should be clearly visible in the epidemic curve, showing an early peak approximately 2 weeks after onset (Hartley et al. 2006). As model runoff is linked to heavy rainfall, this means that the HEH route will only exist when it is raining. Even when new cases of infection occur, and infected waste is dumped on the dumpsites, when it does not rain and the transport mechanism toward the river is missing, river water will remain free of hyperinfectious bacteria.

HEH infected water disappears from the area relatively fast (the water leaves the area within 6.5–13 h). When combining both EH and HEH transmission, we expect that EH transmission determines the onset but HEH soon takes over. Both transmission mechanisms will decline over time due to less susceptible individuals in later phases (Hartley et al. 2006).

The epidemic curve for non-hyperinfectious transmission (without HEH component) builds up infection slowly and maintains itself longer at a more constant rate. According to literature the epidemic curve is flat, and can peak as late as 25 weeks after the first individual is infected (Hartley et al. 2006).

Spatial variations in infections are expected to occur due to differences in number and locations of dumpsites, upstream versus downstream location of communities in comparison to the source of infection and distribution of income classes per community. The location of dumpsites (in relation to the location of the river) can potentially make a large difference in the diffusion process. Also characteristics of the community itself may influence the diffusion pattern. When a community has a high number of higher income households, the river water will not be used. Consequently, the community will remain “safe” and the infection level of the dumpsite will not increase.

2.2.2 Adaptation

In this model the rainparticle agent adapts its direction and speed of movement to the steepness of the terrain and updates its infection level when the path of movement intersects with an infected dumpsite. The individual and household agents do not adapt their behaviour to changing conditions, however, this could be included. Based on awareness of the infection risk, households could change the location where they collect water, increase the hygiene level or buy bottled water.

2.2.3 Objectives

We assume all individuals and households have the objective to stay healthy (not to get infected by cholera). Assuming that water is necessary for everyday life, this may lead to risk avoidance in the type of water a household uses. In this model we make the assumption that households that can afford to buy safe water will do so. The choice to use river water is driven by income level.

2.2.4 Learning and prediction

This model does not include any prediction and does not use any Artificial Intelligence Learning algorithms.

2.2.5 Sensing

Household agents are aware of the location of the river (water fetching points) and the nearest dumpsite. Agents do not sense the level of infection in their community. This means that higher levels of infection do not trigger behaviour change.

2.2.6 Interaction

Rainparticles interact with the dumpsites (can get infected) and households interact with the river (water fetching points) and the dumpsites (dump waste). Indirectly there is interaction between the individuals belonging to a household as they for example share the same water.

2.2.7 Stochasticity

The largest stochastic element in this model is the synthetic population. The process of generating the synthetic population is explained in detail in Sect. 2.3.1. Every time a new population is generated, this will lead to a different collection of households and individuals, living in different spatial configurations. During testing and running of the model, results are always based on a number of iterations that include several different synthetic populations.

Besides the randomness included in the distribution of the population, there are also other random elements in the model that influence the results. As infection is based on a probability, a different number of individuals can get infected even when the population remains the same. In each run of the model, we conduct 10 replicate runs before creating a new synthetic population to account for this variability.

2.2.8 Collectives

A household in this model can be regarded as an intermediate level of organisation. Households are collections of individuals living in the same house. All individuals within a household have their individual variables but are also assumed to share water. This does not mean that all household members will become ill at the same time, as infection is dependent on individual characteristics.

2.2.9 Observations

At a global level we observe the number of susceptible, infected and recovered individuals differentiated by the source of infection (EH or HEH) over simulation time. This allows us to create an epidemic curve for every model run. Information includes the community the infected individual belongs to allowing us to aggregate the number of infections and recovered individuals per community.

2.3 Details

2.3.1 Initialisation

The initialisation of this model can be split into two parts: the loading of the input data (environments and input variables) that will be discussed in 2.3.2 and the generation of the synthetic population (discussed below).

Synthetic population of agents

The study area consists of a water catchment area and does not coincide with administrative boundaries. The area contains 21 communities, of which some communities are completely inside the study area and others only partially (see Fig. 2). The population per community was obtained from Osei (2010). The average number of individuals per household used for the model was 3.9 (GSS 2008). The number of households (67,000) in the study area was calculated based on the community population and average household size. The conducted experiments are based on 8500 households (12.7 % of the actual number) amounting to approximately 33,800 individuals. Because the rain particles are also agents, the combined number of agents in this model will otherwise exceed the capacity of the modelling software (Netlogo).

Fig. 2
figure 2

Left Income levels for the catchment area included in the simulation model. The dots indicate the centre of the communities with labels indicating the community numbers. Right Locations of the dumpsites shown as black dots, and distance zones of 100, 250 and 500 m from the river

Full size image

The synthetic population is generated based on statistical information (aggregated to the community level) obtained from Ghana Statistical Service (2012). Composition of the synthetic population is based on the Monte-Carlo sampling method proposed by Moeckel et al. (2003). In this method, first older people (head of households) are assigned to a household, followed by additional household members. This leads to a natural order of sampling, in which the features of the individuals and households are sampled in the order in which they influence each other. Generating the synthetic population is done by the following steps: (1) creation of the households with household attributes; (2) creation of a set of individuals with assigned characteristics; (3) selection of the head of household (an individual created in step 2) and assigning this individual to one of the households generated in step 1; and (4) Randomly adding additional household members (from the individuals not selected as head of household).

Household variables are hygiene level, income level, access to tap water and household location. Hygiene level consists of three classes (low, medium, high). The size of each of these groups was determined during the calibration phase (Sect. 3.2), leading to a distribution of 19 % (low), 52 % (medium) and 29 % (high), respectively. This is in line with other sources indicating a poverty line of 28 % for urbanised areas outside Accra in 1992 (Devas and Korboe 2000) and 19 % of urban poverty in 1998–1999 (DSDC 2005). Data on access to tap water was derived from national statistical information from the Ghana Statistical Service (2012). As 86 % of the households have access to safe water, this leads to the following division of access to safe tap water over income groups: 100 % for high incomes, 88 % for middle incomes and 78 % for low incomes. Creation of the household variables also includes the selection of a house location.

The spatial distribution of the households is performed via a two-step procedure. First, the correct number of households are assigned to each community. Next, the household is assigned to a particular house, ensuring a match between the income level of the household and the income level of the house. In order to do this, a polygon income level layer (see Fig. 2) is used to assign an income level to each house. This procedure leads to densely and sparsely populated areas.

As the temporal duration of this simulation is only 90 days, the population is static during the simulation process.

2.3.2 Input data

Besides the synthetic population (2.3.1) and the input variables listed in Table 2, we use a DEM which was downloaded from CGIAR website (2010) as a Geotiff image. Flow direction and flow accumulation layers have been calculated based on this DEM using ArcGIS. Houses were digitized based on a Google Earth image of the area of 2006 and refuse dump locations have been collected using GPS. Water fetching points were selected based on flow accumulation greater than the threshold value (Twp). The rainfall data was obtained from the Tutiempo Network SL, providing daily recorded rainfall data from September 30 to November 30, 2005. As no hourly rainfall information is available, the assumption was made that the duration of rainfall is 2 h per day. The income levels (Fig. 2) are polygons digitized based on expert knowledge in combination with building characteristics.

Table 2 Values of variables related to the synthetic population, hydrological sub-model and the disease sub-model used for calibration of the complete model (min, max) and the selected value (value)
Full size table

2.3.3 Sub-models

Disease sub-model

The probability of a household using contaminated water is influenced by the likelihood the household has to fetch water from the river. The likelihood that the household has to get water is influenced by two factors: income level (higher incomes are supposed to buy water) and rainfall. During heavy rainfall there may be no tap water due to power shortage in Kumasi. In the model this is accounted for by introducing a threshold rainfall (Pmax) beyond which tap water stops working and more households will be forced to use river water.

There are two types of contaminated water (EH and HEH). The probability of fetching EH contaminated water, Pfeh, is set to 3 % (see Sect. 3.2).

The probability of fetching HEH contaminated water depends on the runoff from infected dump sites and the travel time and varies in space and time. It is assumed that after dumping infected waste, the infection level, D, of the dumpsite will increase by 1. Dumpsites will start to induce runoff particles with hyperinfectious bacteria when the dumpsite infection level is above the threshold, Dmax. Literature indicates that V. cholerae populations have an extinction rate ranging from 0.02 days to >3 days (Codeço 2001; Feachem et al. 1983). Conditions on dumpsites may vary in relation to temperature and humidity. Two options are built into the model: dumpsite infection level without and with a decay function. In case of no decay, once infected, the dumpsite will remain infected until the end of the simulation. For the option with dumpsite infection decay:

$$D_{t + 1} = D_{t} - \left( {\frac{{D_{t} }}{{D_{decay} }}} \right)$$
(1)

in which Ddecay is a decay constant (>1), and t is the time step (hour). Infection can take place when individuals that are susceptible drink water in a household that has fetched contaminated water. The probability for an individual to get infected by drinking contaminated water (P) is calculated as:

$$P = \left( {P_{ch} + P_{ew} } \right)$$
(2)

In which Pch is the probability of infection based on household and individual characteristics and Pew is the probability of getting infected due to drinking contaminated water independent of the characteristics. One of the individual characteristics that determines the probability of infection is blood type, assuming a higher risk for individuals with blood type O (Holmner et al. 2010). Relevant household characteristics are hygiene level and income level (see Table 3).

Table 3 Relationship between the household and individual characteristics (hygiene level, income level and blood type) and the probability of infection (Pch)
Full size table

When simulating a river system covering a larger area, river water will remain in the study area long enough for the transition of a hyperinfectious state to lower infectiousness. However, this is not the case for areas the size of our case study area making the transition mechanism redundant. We found that water leaves the area within a time frame of 6.5–13 h. This is faster than the hyperinfectious state persistence of up to 24 h documented by Harris et al. (2012).

Hydrological sub-model

The hydrological sub-model simulates the downstream transport of hyperinfectious bacteria from dumpsites. In order to simulate surface water flow, a DEM, flow direction layer and a flow accumulation layer are loaded into the model. Water is simulated as rain particles (agents) flowing over the DEM surface. The amount of surface runoff is based on actual rainfall data for the case study area. The volume of water per rain particle is calculated by dividing the total volume of rain by the number of rain particles. The flow direction layer is used to determine to which neighbouring cell a rain particle will flow using the steepest downhill slope.

In this model the travel time of rain particles, T is calculated using the general Manning formulas. Three different types of flow are used: sheet flow (sf), gully flow (gf) and river flow (rf), corresponding to different travel times. We determine which type of flow applies by using the flow accumulation. For sheet flow (patches with flow accumulation <Sgf) travel time is calculated by SCS (1986):

$$T = 184\frac{{\left( {F_{L} m_{sf} } \right)^{0.8} }}{{P^{0.5} S^{0.4} }}$$
(3)

where msf is the Manning coefficient for sheet flow (m−0.375 h1.25), FL is the flow length (m), P is the rainfall (m) and S is the slope in (m/m). For gully flow (patches with flow accumulation ≥Sgf and <Srf) and river flow (flow accumulation ≥Srf) the Manning formula for channel flow will be used (Shaw et al. 2011):

$$T = \frac{{F_{L} m_{c} }}{{R^{2/3} S^{1/2} }}$$
(4)

in which R is the hydraulic radius (m), i.e. the cross sectional flow area divided by the wetted perimeter and mc is the Manning coefficient for open river channel flow (m−1/3 h). FL, msf, (R2/3/mc) for gully and river, Sgf and Srf and S are determined in the calibration process (Table 4).

In case rain particles travel only part of a cell (during a particular time step) this is accounted for by storing the remaining travel distance in memory and adding this travel distance to the distance travelled during the next time step.

Table 4 Values of variables used during the calibration of the hydrological sub-model
Full size table

2.4 Model output

In many models the basic reproduction number (R0) is taken as measure to quantify the epidemic. However, R0 is known to be very sensitive to input parameters of a model (Grad et al. 2012) and some of the parameters used are also not obvious in our model. We also think that the spatial patterns should be considered as our model is spatially heterogeneous.

The model provides output on the level of the individual (e.g. time step in which individual was infected and recovered, including the type of infection, EH or HEH), of the community (epidemic curve per community), of the dumpsite (infection level at a certain time step) and of the total population (epidemic curve). The data available to compare the simulation results to are the number of cholera patients per community registered by the Disease Control Unit (DCU).

The model performance will be based on the relative diagnosed disease cases per community in percentage:

$$GD = \frac{Number\, of\, cases \,in \,community}{Total\, number \,of \,cases}{ \times }100$$
(5)

Model performance will be determined by comparing the simulated percentage of disease cases in each community (GDs) to the percentage of diagnosed disease cases in the 2005 outbreak (GDd). The accuracy of the simulations will be expressed as r2 (with r2 = 1 a perfect simulation), where r is the Pearson’s correlation coefficient defined as:

$$r = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left( {GD_{s,i} - \overline{{GD_{s} }} } \right)\left( {GD_{d,i} - \overline{{GD_{d} }} } \right)} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {GD_{s,i} - \overline{{GD_{s} }} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {GD_{d,i} - \overline{{GD_{d} }} } \right)^{2} } }}$$
(6)

where i refers to community i and n is the number of communities. The hydrological model requires the study area to be a catchment area. As a consequence, delineation of the case study area does not coincide with administrative boundaries. In this area we have 21 communities of which 11 are completely within the study area and 10 only partially. The value of r2 is calculated for the 11 communities completely inside and for the total 21 communities (r2*).

The spatial element is contained in the fact that for every community the simulated percentage of cases is compared to the observed number of cases in that community. By doing so, the overall spatial pattern can be evaluated.

In addition we evaluate the time of first infection and duration of infection per community.

3 Model implementation

3.1 Case study

The model is implemented in Netlogo version 5.05 and initialized with a subarea of the city of Kumasi, Ghana. Kumasi is a metropolis located in the Ashanti Region. It is a fast growing regional capital with a population in 2013 of 2,069,350 people (World-gazetteer.com). Kumasi consists of a number of communities with no exact geographic boundaries. Disease cases are registered per community.

Living and housing conditions in many of the communities are overcrowded (Whittington et al. 1993). This is mainly because of rapid urban population growth. Poor housing conditions reflect high probability of low incomes. The city of Kumasi experiences different raining seasons, a longer raining season from March through July and a shorter raining season from September to November. The cholera epidemic of 2005 started during the short raining season and covers a period from September to December. During this period, water shortages occurred due to the low power voltage (DNA 2010). During these water shortages, most households used surface water from rivers and streams for drinking, cooking, and other household activities (Osei et al. 2010).

The study area does not include the complete Kumasi area but was restricted to one catchment in the centre of the city.

3.2 Model parameterisation and calibration

Calibration has been conducted in two steps: first the hydrological sub-model was calibrated, followed by a calibration on the complete model. After the calibration a stability check was performed.

For the calibration of the hydrological sub-model the simulated discharge was compared to the discharge calculated by the Curve Number method (CN) (Boonstra 1994). The CN method is widely used (Arnold et al. 1998; Boonstra 1994) to simulate surface runoff. The range of parameters used in this calibration are shown in Table 4. After calibration of the parameters in the manning equations, the agent-based hydrological model showed good agreement with the discharge generated by the Curve Number method (see Fig. 3). The simulated average velocity for river flow was 0.65 m/s and for gully flow 0.35 m/s, which are in the correct order of magnitude (Riscassi and Schaffranek 2003). A detailed description of the calibration goes beyond the objective of the paper. For more information see Doldersum (2013).

Fig. 3
figure 3

Discharge of the simulation model (simulated discharge) compared to the discharge calculated by the CN method for the duration of the simulation. Rainfall is included as green crosses

Full size image

The dataset used for the calibration of the complete model consisted of cholera cases for the 2005 epidemic. All cases were confirmed by bacteriological tests and were reported to the disease control unit (DCU). Not all communities have a hospital but all have clinics or community volunteers.

Calibration of the complete model was done globally using a Monte Carlo simulation after selecting ranges for all parameters. Every parameter was varied randomly within the range, after which r2 was calculated. The range of values was narrowed until the r2 showed no further improvement. The final parameter values after calibration, including the ranges of values used during the calibration are shown in Table 2.

The value for the probability of fetching EH contaminated water (Pfeh) was determined by running the model with a range of input values (1–6 %) and selecting the lowest value at which spontaneous infection occurred and rainfall influence due to lack of tap water was visible. Contrary to other models, this value is constant during the simulation. Results are shown in Fig. 4.

Fig. 4
figure 4

Calibration of the probability of fetching water contaminated with EH (Pfeh) by varying the value between 1 and 6 %

Full size image

The stability check was conducted by running the model 250 times, creating a new population every 10 runs, and checking when values became stable. The check was conducted for EH only, for HEH (including EH) without dumpsite decay and with dumpsite decay. The model became stable after approximately 100 runs (see Fig. 5).

Fig. 5
figure 5

Stability checks for EH, HEH (without decay) and HEH with decay, showing the r2 calculated over an increasing number of simulation runs (10–250)

Full size image

4 Results

Two sets of experiments are conducted to test the hypothesis of dumpsites playing a role in the diffusion of cholera during the 2005 outbreak in Kumasi. In the first experiment the model is tested under three conditions: EH transmission (Sect. 4.1), HEH transmission without decay and HEH transmission with decay of the infection level of the dumpsites (4.2).

In the second experiment, we test the assumption that it is possible that only part of the dumpsites actively contributed to the diffusion process (4.3). We do this by selecting only dumpsites that are within a certain distance (100, 250 and 500 m) from the river for the HEH runs. Distances were selected based on findings of Osei and Duker (2008), indicating that 500 m is the range within which a spatial dependency exists between cholera and refuse dumps.

All experiments are influenced by the synthetic population; therefore each experiment is repeated 100 times, generating a new synthetic population for every 10 runs.

4.1 EH transmission

The EH transmission experiment benchmarks the situation without hyperinfectious V. cholerae diffusion. In this case, infection only takes place via natural V. cholerae and is independent of the number of infected individuals. However, the number of people that are exposed to contaminated water will vary, as the number of people dependent on river water varies as a result of tap water availability during the simulation.

Results from a global perspective are included in Table 5 and the epidemic curve is shown in Fig. 6. The r2 for this experiment is 0.69 indicating some resemblance to the spatial pattern in the 2005 dataset. As the probability of getting infected is the same throughout the study area, this resemblance can only be explained by the distribution of the population in space.

Table 5 Results of the experiments showing mean number of cases, r2 for the communities located completely in the study area and all communities, r2*, and number of infected dumpsites
Full size table
Fig. 6
figure 6

Epidemic curves for EH (top), for HEH (middle) and for HEH with decay of dumpsite infection level (bottom). Blue line showing the mean epidemic curve (100 runs) with, in light blue, the variation between the runs. Black bars indicate the days and intensity of the rainfall. Vertical scale of EH differs from scale of HEH and HEH decay

Full size image

The epidemic curve (Fig. 6) shows a weak peak after 33 days (approximately 5 weeks) and infection persists throughout the simulated period with a decline to a minimal number of infections after 80 days (approximately 11 weeks), resembling a more endemic situation, similar to results obtained by Hartley et al. (2006). The epidemic curve shows a weak response to rainfall which can be attributed to a higher number of households being exposed, due to malfunctioning of tap water.

When evaluating the boxplots of the individual communities (Fig. 7) we see that for a number of communities (1, 2, 5, 12, 19) the relative number of cases is underestimated. These communities are located both in the upstream and downstream parts of the study area and are all completely within the study area. For these communities, hyperinfectiousness may have played a role. Overestimation takes place in communities 9, 10, 16 and 21. Where communities 9 and 10 are located downstream, communities 16 and 21 are located in the upstream area. Communities 9, 10 and 16 are only partially within the study area.

Fig. 7
figure 7

Boxplots for EH (left), HEH (middle) and HEH with decay (right) showing the percentage of cases (top), the day of first infection (middle) and the duration of infection (bottom) per community. Red dots indicate the values during the 2005 epidemic

Full size image

The timing of the first infection and duration of infection in the simulated results show an earlier onset of the epidemic (faster infection) compared to the empirical data. The simulated duration of infection is longer compared to the empirical data for the communities of the study area.

4.2 HEH transmission

In the HEH experiment (without decay) the r2 increases to 0.86 (Table 5), showing a closer resemblance of the spatial pattern found in the empirical data compared to EH. The epidemic curve shows a clear response to the rainfall (peak with onset on day 23) as can be seen from Fig. 6.

The pattern at the level of the communities (Fig. 7) shows that we have an underestimation in the communities 1, 2 and 5 and an overestimation in 9, 10 and 21. These are the same communities showing over/underestimation in the EH experiment. Patterns for onset of infection and duration of infection show earlier first infection and longer duration compared to the empirical data.

For the experiment with a decay function, the r2 is 0.81 which is slightly lower than in the experiment without decay, with a small decline in the number of infected individuals from 2773 to 2208. The relative contribution of the EH transmission route is 22 % in the experiment with decay compared to 15 % in the experiment without decay. The epidemic curve of the simulation with decay differs from the experiment without decay in that the variability between the individual runs is much larger (see Fig. 6). When we compare the boxplots of the communities (Fig. 7) the first infection and duration of infection are similar except for a few small deviations.

4.3 Distance

In the previous experiments it was assumed that all dumpsites played a role in the diffusion process. However, it is likely that runoff from dumpsites that are located closer to the river will reach this river more often, compared to runoff from more distant dumpsites due to stagnation and infiltration of water. For both HEH transmission experiments (with and without decay) we have conducted runs in which we only included dumpsites within a certain distance from the river (100, 250 and 500 m). For the results see Fig. 8 and Table 5.

Fig. 8
figure 8

Epidemic curves for the distance experiments, on the left the experiments for HEH and on the right the experiments for HEH with decay. On top the results with only dumpsites within 100 m from the river, in the middle dumpsites within 250 m, and bottom dumpsites within 500 m

Full size image

When including only dumpsites within 500 m from the river, this leads to an r2 value for HEH with and without decay of 0.80 and 0.87, respectively. These results are similar to including all dumpsites. This implies that dumpsites further than 500 m from the river did not play a role in the runoff. However, as the study area is small, only three dumpsites are located outside this buffer distance (see Fig. 2). The observed effect can also be the result of a mismatch in time it takes runoff to reach the rivers and water fetch time. When this runoff time is long and the water fetching has already been completed for the particular day, this can result in a similar effect. When restricting the distance further to 250 and 100 m, the r2 value becomes lower. This is probably due to the fact that the number of dumpsites included drops considerably.

When we compare the r2 (in which only the 11 communities that are completely within the study area are included to the results of r2* in which all 21 communities are included, we see that the pattern remains the same although the values are consistently lower.

5 Discussion

Even in the experiments with only EH, we see a reasonable r2 of 0.69. This is unexpected given the simple structure of the EH model, with a constant infection probability, the omission of hyperinfectiousness and the fact that we minimized the Pfeh value (determined via calibration). We believe this is caused by the structure of the population and in particular by the distribution of the population in space. While generating the synthetic population, we controlled the number of individuals in each income group and by doing so, we indirectly influenced the number of potentially exposed individuals, as higher incomes are assumed to have access to clean water and lower income groups resort to using river water more often. This was reflected in the spatial distribution of the households, meaning that we generate communities with a large percentage of higher income households, and communities with a large number of lower income households at the correct location. This confirms the dependency of cholera transmission on the socio-economic structure of the area but also underlines the importance of spatially explicit models.

In the results we see higher r2 values and more realistic epidemic curves for the situation with hyperinfectiousness compared to the EH experiments. This confirms that hyperinfectiousness played a role in the 2005 Kumasi outbreak. In the model we were able to model the hyperinfectiousness via runoff from infected dumpsites. The results show that dumpsites within 500 m from the river contributed to the diffusion (as we see no significant difference in the r2 between the experiments including dumpsites within 500 m and all dumpsites), but also show that this must have been a fairly common diffusion route in which most dumpsites play a role (when we reduce the distance, and therefore the number of contributing dumpsites, the r2 decreases).

The model we used in this research has a hydrological sub-model that requires the case study area to coincide with a hydrological catchment. In our situation, a part of the communities extended beyond the catchment boundary. As a result the comparison between the empirical data and simulated cholera incidences was more difficult, forcing us to calculate the r2 including only the communities completely located within the catchment, and the r2* including all communities. For the communities that are partially outside the study area, the recorded diagnostic data may refer to individuals living outside the catchment. This is reflected in lower values of the r2* compared to the r2 values. Because no exact administrative boundaries of the communities are known, correction for this issue was not possible.

In general, parameterization of cholera models is believed to be difficult because many important factors are unknown, like the exposure to contaminated water, the concentration of V. cholerae in the river water, the decay of the infectious vibrios and the infectious dose (Grad et al. 2012). For the 2005 Kumasi outbreak, no micro-biological data is available to make reliable estimates. We have therefore chosen to create a simplified model solely meant to test the runoff transmission route hypothesis and to analyse the results based on general spatial and temporal patterns.

The model itself contains some clear limitations which are mainly linked to the limited behaviour of the agents. Agents collect water only once a day at a fixed time step creating a sensitivity to the order in which the processes are scheduled (rain versus fetching of water).Movement of agents to other locations within the study area is currently not modelled. Most important limitation of the model is probably the fact that agents that collect river water, do so at a fixed water point (closest to their home) without evaluating the risk of using this water. Evaluation of risk can be based on media attention, knowledge about disease cases in their neighbourhood, or even spatial intelligence (water upstream from dumpsite is cleaner). Extending this model with an artificial intelligence component that enables agents to evaluate their risk and change their behaviour could address these limitations.

6 Conclusions and recommendations

This work proposes an ABM for micro-simulation of cholera diffusion, that incorporates an environmental reservoir of natural V. cholerae (EH mechanism) and diffusion of hyperinfectious V. cholerae via runoff from dumpsites. The proposed model is simple in its setup and can be extended by adding new elements like human movement and change of behaviour of individuals based on disease awareness (avoid using river water).

The model output showed a good correlation to the spatial–temporal pattern of the 2005 outbreak in Kumasi, Ghana. The correlation of the EH transmission depended mainly on the quality of the synthetic population and more precisely on the spatial distribution of the different income groups. Model output was improved by adding the HEH transmission, indicating that hyperinfectiousness played a role. This may have been caused by runoff of dumpsites within 500 m from the river, although in this case, a large number of the dumpsites contributed to the infection.

ABMs seem to be a good choice for simulating the spread of a disease like cholera where both environmental processes and human behaviour are allies in the diffusion mechanism. ABMs are especially suitable for micro-simulation and this type of simulation can lead to new understanding of underlying diffusion mechanisms. A complete validation of an agent-based cholera model will be difficult to achieve, as this would mean that not only V. cholerae ecology and epidemiology but also human behaviour will have to be validated, and it is arguable if this will ever be possible. However, if specific spatial and spatial–temporal patterns can be found that are reproducible via pattern-oriented modelling, good results might be achieved.

This research shows the potential health effect of open dumpsites in Kumasi, but the problem of improper solid waste disposal is widespread in many other cities in developing countries. Besides relating to cholera, open dumpsites can also have other health effects. Results stress the importance of proper solid waste disposal, which could lead to relocating open dumpsites, conversion to covered landfills or improved waste collection systems. Solving the cholera problem requires equal attention to proper sanitation and access to clean water.