Latent period in induction of radiogenic solid tumors in the cohort of emergency workers

Abstract

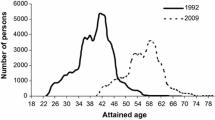
The paper presents estimates for the latent period of the induction of radiogenic solid cancers among Chernobyl emergency workers (males) living in six central regions of Russia. The analysis is based on medical and dosimetry data gathered by the National Radiation and Epidemiological Registry over the time period from 1986 to 2005. The cohort includes 59,770 persons who stayed in the exposure zone (30-km zone around the Chernobyl nuclear power plant) in 1986–1987. There were 2,718 cases of solid tumors identified during the follow-up time in this cohort. The mean radiation dose in the cohort is 0.13 Gy. The radiation risk and latent period were estimated using the method of maximum likelihood. The excess relative risk per unit dose was found to be 0.96 (95% confidence interval (CI): 0.3–1.7) and the minimum latent period for induction of solid tumors is 4.0 years (95% CI: 3.3–4.9).

Appendix 1

If the number of unknown quantities θ ₁, θ ₂,…,θ _p is more than one, the joint sample distribution of the likelihood maximum estimate is asymptotically normal, with the mathematical expectancy θ ₁ , θ ₂ ,…,θ _p and the covariance matrix A ⁻¹ (Lederman 1984), where the (r,s)-th element of the matrix A is approximately equal to $\frac{{ - \partial^{2} { \ln }(lik)}}{{\partial \theta_{r} \partial \theta_{s} }},$ s, r = 1,2,…,p.

In case of two unknown quantities the covariance matrix of the likelihood maximum estimate can be written as (9):

$$ \left[ {\begin{array}{*{20}c} {\sigma_{1}^{2} } & {\rho \sigma_{1} \sigma_{2} } \\ {\rho \sigma_{1} \sigma_{2} } & {\sigma_{2}^{2} } \\ \end{array} } \right], $$

(9)

where $\sigma_{1}^{2} ,\sigma_{2}^{2}$ are the sample variances of the estimates $\hat{\theta }_{1} ,\hat{\theta }_{2} ,$ and ρ is the sample correlation coefficient.

Then, the approximate covariance matrix will take the form shown in (10) (−1 is the sign of the reverse matrix):

$$ - \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \,{ \ln }(lik)}}{{\partial \theta_{1}^{2} }}} & {\frac{{\partial^{2} \,\ln (lik)}}{{\partial \theta_{1} \partial \theta_{2} }}} \\ {\frac{{\partial^{2} \,{ \ln }(lik)}}{{\partial \theta_{1} \partial \theta_{2} }}} & {\frac{{\partial^{2} \,{ \ln }(lik)}}{{\partial \theta_{2}^{2} }}} \\ \end{array} } \right]^{ - 1} $$

(10)

The elements of matrix (10) are written as given in 11, 12 and 13:

$$ \frac{{\partial^{2} \,{ \ln }(lik)}}{{\partial \beta_{1}^{2} }} = \sum\limits_{j = 1}^{m} {\frac{{B^{2} (T)_{j} }}{{(A_{j} + \beta \cdot B(T)_{j} )^{2} }} - } \sum\limits_{j = 1}^{m} {\frac{{S^{2} (x_{j} )d_{j}^{2} }}{{(1 + S(x_{j} )\beta d_{j} )^{2} }}} $$

(11)

$$ \begin{aligned} \frac{{\partial^{2} { \ln }(lik)}}{{\partial T_{2}^{2} }} = & \beta \sum\limits_{j = 1}^{m} {\frac{{S^{\prime\prime}(x_{j} )d_{j} }}{{1 + \beta S(x_{j} )d_{j} }}} - \beta^{2} \sum\limits_{j = 1}^{m} {\frac{{S^{'2} (x_{j} )d_{j}^{2} }}{{(1 + \beta S(x_{j} )d_{j} )^{2} }}} \\ & \quad - \beta \sum\limits_{j = 1}^{m} {\frac{{B2(T)_{j} }}{{A_{j} + \beta B(T)_{j} }}} + \beta^{2} \sum\limits_{j = 1}^{m} {\frac{{B1^{2} (T)_{j} }}{{(A_{j} + \beta B(T)_{j} )^{2} }}} \\ \end{aligned} $$

(12)

$$ \frac{{\partial^{2} \,{ \ln }(lik)}}{{\partial \beta_{1} \partial T}} = \sum\limits_{j = 1}^{m} {\frac{{S^{\prime}(x_{j} )d_{j} }}{{(1 + \beta S(x_{j} )d_{j} )^{2} }} - } \sum\limits_{j = 1}^{m} {\frac{{B1(T)_{j} A_{j} }}{{(A_{j} + \beta B(T)_{j} )^{2} }}} $$

(13)

where $B2(T)_{j} = \sum\limits_{i = 1}^{N} {\sum\limits_{k = 1}^{{t_{i} }} {{\text{PY}}_{{g_{i} + k}} } } S^{\prime\prime}(x_{j} )d_{i} .$

The approximate joint confidence region for the quantities β and T of the ellipse shape is written as in (14) (Lederman 1984):

$$ \frac{{(\beta - \hat{\beta })^{2} }}{{\sigma_{\beta }^{2} }} - \frac{2\rho }{{\sigma_{\beta } \sigma_{T} }}(\beta - \hat{\beta })(T - \hat{T}) + \frac{{(T - \hat{T})^{2} }}{{\sigma_{T}^{2} }} = \gamma (1 - \rho^{2} ), $$

(14)

where the coefficient γ defines the boundaries of the confidence region.

The values $\hat{\beta },\hat{T}$ are the estimates of the quantities derived by solving the system of equations (8). The value γ is found from (15):

$$ 1 - e^{ - \gamma /2} = \xi . $$

(15)

For the 95 % confidence interval ξ = 0.95, the value γ = 5.99.

Hence, all the values of β and T for which the left side of (14) is less than the right one, will occur within the joint confidence region.