INTRODUCTION
Salmonella spp. are frequently isolated from dairy cattle and from various locations within dairy farm environments such as water, feed, manure, and bird droppings. Salmonellosis (the clinical disease caused by Salmonella spp.) can have serious health implications in calves and cattle, but asymptomatic shedding in faeces also occurs [Reference Warnick1]. There are more than 2000 known serotypes of S. enterica. The NAHMS Dairy 1996 study showed faecal shedding of Salmonella in 5·4% of cows [Reference Wells2]. The most common serotypes isolated from the faecal samples were Montevideo (21·5%), Cerro (13·3%), Kentucky (8·5%), Menhaden (7·7%), Anatum (6·1%), Meleagridis (6·1%), Muenster (4·7%), and Mbandaka (4·6%). Although the most common salmonellae that cause disease in humans (United States) are S. enterica Typhimurium, Enteritidis, and Heidelberg, all Salmonella are potentially pathogenic.
Presence of Salmonella enterica serotype Cerro (S. Cerro) has been described in several reports from wildlife, food animals, and occasional cases of disease in humans. Specifically, isolations of this serotype have been described from hens' eggs [Reference Saitanu3], duck eggs [Reference Saitanu, Jerngklinchan and Koowatananukul4], captive crocodiles [Reference Manolis5], poultry flock and slurry [Reference Sunaga and Sato6, Reference Riemann7], and from asymptomatic dairy and beef cows [Reference Dargatz8, Reference Beach, Murano and Acuff9] and bulk tank milk [Reference Van Kessel10]. In humans, S. Cerro was isolated from healthy schoolchildren [Reference Devi and Murray11] and occasional cases of disease [Reference Bhore, Phadke and Joshi12–Reference Mammina15]. A European surveillance study reported the endemic presence of S. Cerro in Southern Italy. Human sources (both healthy and diseased), food items, environmental samples and urban sewage plant effluents were positive for this serotype. In this particular environment, S. Cerro prevalence was ranked second only to S. Typhimurium.
Studies from dairy farms such as the one reported by Peek et al. [Reference Peek16] showed the presence of S. Cerro in environmental samples from 1 of 20 herds in Wisconsin. These free stall dairies had no history of clinical salmonellosis. Van Kessel et al. [Reference Van Kessel10] reported in results from 860 dairies from 21 states participating in the 2002 NAHMS study. They observed S. Cerro in the bulk milk of two of these dairies [Reference Van Kessel10].
Modelling of S. Cerro infection patterns within the herd would help to explain the population dynamics and clarify the reason why this organism is able to maintain itself in herds. Modelling of infectious disease in dairy herds has been done before (see e.g. [Reference Lam17, Reference Hage18]) and often resulted in a better understanding of infection dynamics. Results of these studies were used to design vaccination programmes or to facilitate eradication of the infection from the herd. Salmonella infections have been modelled before [Reference Xiao19], using a SIRS model stratified for age and lactation period (dry vs. lactating). The model was used to perform simulations, but was not tested against observed data. In this case study we report the observed endemic presence of S. Cerro on a dairy farm. Our objective is to apply a modified version of the SIR model [Reference Anderson and May20] and the Xiao et al. model [Reference Xiao19] to the observed data to study the cause of S. Cerro endemicity of this infection within the herd.
MATERIALS AND METHODS
Farm description
The dairy farm where the samples for this study were collected participates in a multi-state research programme conducted under a cooperative research project between the Regional Dairy Quality Management Alliance (RDQMA) and the Agricultural Research Service (ARS). The farm is located in Pennsylvania and milks ~100 cows. Heifer calves are born on the farm and at ~6 months of age are moved to a contract heifer grower with heifers returning to the farm prior to calving. Participation in the study includes quarterly blood sampling of all lactating animals and bi-annual faecal sampling.
Sampling, sample handling, sample analysis, definition of infection
After the initial detection of salmonella infection on the farm, the faecal sampling frequency was increased and all cows were sampled every 6–8 weeks for ~1 year. Faecal samples were obtained by rectal palpation and placed directly into sterile vials, cooled, and transported overnight to the Environmental Microbial Safety Laboratory of the Agricultural Research Services in Beltsville, Maryland. Upon arrival, ~25 g of faecal material was weighed into a filtered stomacher bag, diluted (2/1) with buffered peptone water (1%) and pummelled in an automatic bag mixer for 2 min. For enrichment of salmonella, 5 ml filtrate was added to 5 ml double-strength tetrathionate broth and incubated at 37°C for 24 h. Enrichment tubes were incubated at 37°C for 24 h and then the broth was streaked (10 μl) onto XLT4 agar (XLT4 agar base with XLT4 supplement, BD Diagnostics, Sparks, MD, USA). Plates were incubated at 37°C and scored at 24 h and 48 h for presumptive salmonella (black colonies). Isolated, presumptive salmonella colonies were transferred from XLT4 plates onto XLT4, Brilliant Green, and L-agar (Lennox Broth base with 1·5% agar; Gibco Laboratories, Long Island, NY, USA). Colonies that exhibited the salmonella phenotype (black on XLT4 and pink on Brilliant Green) were preserved for future analysis. The isolates were stored at −80°C. For some of the isolates, L-agar slants were inoculated and, after incubation at 37°C for 24 h, sent to the National Veterinary Services Laboratories in Ames, IA, USA for serotyping. The serotypes of other isolates were determined with rep-PCR using the ERIC primers as described by Weigel et al. [Reference Weigel21]. An isolate with an ERIC-PCR pattern that was similar to a pattern of an isolate serotyped by NVSL was considered that serotype. Not all isolates were serotyped. Culture procedures used in this analysis have an approximate sensitivity of 1 c.f.u./g faeces.
For PCR analysis, biomass from the enrichments was stored at −20°C. The DNA was extracted from these pellets using Mo Bio UltraClean Soil DNA Extraction kits (Mo Bio Laboratories, Inc., Carlsbad, CA, USA) following the manufacturer's directions. The DNA preparations were stored at −20°C and were analysed for the presence or absence of salmonella via real-time PCR at a later date. Real-time PCR was carried out using an adapted conventional PCR method of Rahn et al. [Reference Rahn22] and shown by Malorny et al. [Reference Malorny23] to detect a wide range of salmonellae. The method was adapted for real-time PCR by the addition of SYBR Green to the assay. Theoretically, this PCR method has an approximate sensitivity of 1 c.f.u./3 g faeces.
For the purpose of this analysis, records of all cows and all samples were combined and displayed longitudinally. We assumed a non-perfect sensitivity and therefore occasional negative faecal culture results were expected even in truly infected animals. For that reason, animals were considered truly longitudinally infected if two of three subsequent samples were faecal-culture positive. An animal was considered negative after a previous infected period when at least two subsequent samples were culture negative. Hence, in some instances the calculated adjusted prevalence of infectious animals was somewhat different from the actual faecal culture-positive prevalence on a specific sampling day. The difference was due to animals that were culture positive before and after this particular sampling day but were negative on this day. To estimate the rate of new infections, the occurrence of a new infection was placed at the midpoint between two sampling days where the first sampling day was negative and the second was culture positive. Each animal contributed days at risk of infection calculated on a daily basis and using the infection assumptions described above.
MODEL FORMULATION
The mathematical model we used was a state-transition model and was adopted from Xiao et al. [Reference Xiao19]. As with traditional SIR modelling, the animals in the herd are grouped into three compartments according to their salmonella infection status – those which are susceptible (S), those infected with salmonella and are infectious (I), and those which are recovered from the infection (R). The total number of animals in the herd is given by N=S+I+R. In the present model, we consider that initially all the animals are susceptible to the infection. Once infected, a susceptible individual leaves the susceptible compartment and enters the infectious compartment where it too becomes infectious. The infected animals pass into the recovered compartment unless they exit the herd for other reasons such as death or culling. Because of the high prevalence shortly after the onset of the infection and unusually long persistence of the infection observed in the herd, the latent period is not considered in the model. The loss of immunity is incorporated by allowing animals to pass back into the susceptible compartment from the recovered class. The average rates of entry and exit from each compartment and other relevant parameters calculated from the data, collected from literature, or assumed are summarized in the Table.
Table. Definition and the parameter estimates for the transition rates and other parameters in the model that describes the transmission dynamics of Salmonella Cerro infection in a dairy herd. The transmission rates are given in units of per month
An important difference in this model from other models describing salmonella dynamics [Reference Xiao19, Reference Ivanek24] is the consideration of a more realistic distribution of per capita recovery rate, γ. Classical SIR models simply assume an exponential distribution of infectious period, with mean duration of infection equal to 1/γ. While it has been commonly believed that the precise distribution of the infectious period is unimportant, some recent studies show that it has important consequences in the dynamics of infection [Reference Mittler25–Reference Lloyd27] and the model results. In this study, a more realistic distribution of the infectious period, namely a gamma distribution, is included and the model is validated with the actual observed dynamics in the herd. This is especially important when considering the prevalence of infection in a herd-level population as the exponential distribution of infectious period tends to yield unrealistically low prevalence of infection and takes longer [Reference Wearing, Rohani and Keeling28] for the infection to die out in the herd.
The infectious period distribution can be described in terms of the probability distribution function, p(τ), which gives the survivorship function, P(l), upon integration:
The survivorship function gives the probability for an individual to remain infectious for at least l time units. As opposed to the exponential distribution of the infectious period, a more realistic probability density function, p(τ), of the infectious period can be incorporated in the differential equations. This can be done by the method of multiple stages [Reference Lloyd27] in which the single infectious compartment of the classical SIR model is replaced by n successive infectious compartments, each with an exponential distribution of the same value of the mean infectious period, 1/γ, with nγ as the rate of progression through the series of the states. Thus the total time spent in the n compartments is just the sum of n exponential distributions. This gives the gamma distribution of the infectious period with the probability density function [Reference Lloyd27]:
where Γ(n) is the gamma function. The exponential distribution of the infectious period in the classical SIR model is retained when n is set to 1. Since the variance of this distribution is given by 1/(nγ2), it is easy to estimate the number of compartments that should replace the otherwise single infectious compartment so that the variance of the observed distribution of infectious period can be more accurately incorporated in the model.
In order to model the possible indirect transmission due to free-living bacteria in addition to the direct animal-to-animal transmission, we also include the density of the pathogen in the environment. A simplifying assumption was made that all infected individuals shed pathogen into their environment at an equal rate in order to keep the model less complex. Therefore, the density of the bacteria in the environment (W) is simply a function of the number of infected animals shedding the bacteria and the bacterial survival rate in the environment. Here, we make no distinction between local and combined environment [Reference Xiao19] and treat W as the total density of the bacteria in the environment.
The dynamics of host and pathogen is modeled using a set of nonlinear differential equations which is a modified version of the SIR model. The mathematical equations that incorporate the method of multiple stages [Reference Lloyd27] in the model are given as:

Here, I is the total number of infective animals which is given by the sum of all infective animals in various infectious stages, ![]() . The rates of transition between various compartments and other parameters are defined in the Table and the transmission dynamics described by the above system of nonlinear equations is depicted in Figure 1.
. The rates of transition between various compartments and other parameters are defined in the Table and the transmission dynamics described by the above system of nonlinear equations is depicted in Figure 1.

Fig. 1. Flow diagram representing the transmission dynamics of S. Cerro infection in a dairy herd modelled by the system of equation (3). Parameters are defined in the Table, the compartments are defined as: S is susceptible, I i is infectious (i=1, … , n), R is immune and W is the environment.
The transition rates were estimated from the adjusted faecal culture data. The distribution of the infectious period was fitted with the gamma distribution in order to calculate the average infectious period, 1/γ, and variance of the distribution, 1/(nγ2), where γ is rate at which an infected individual recovers from the infection. These two quantities give the number of stages that the single infectious compartment needs to be divided in the model described by the set of equations [equation (3)].
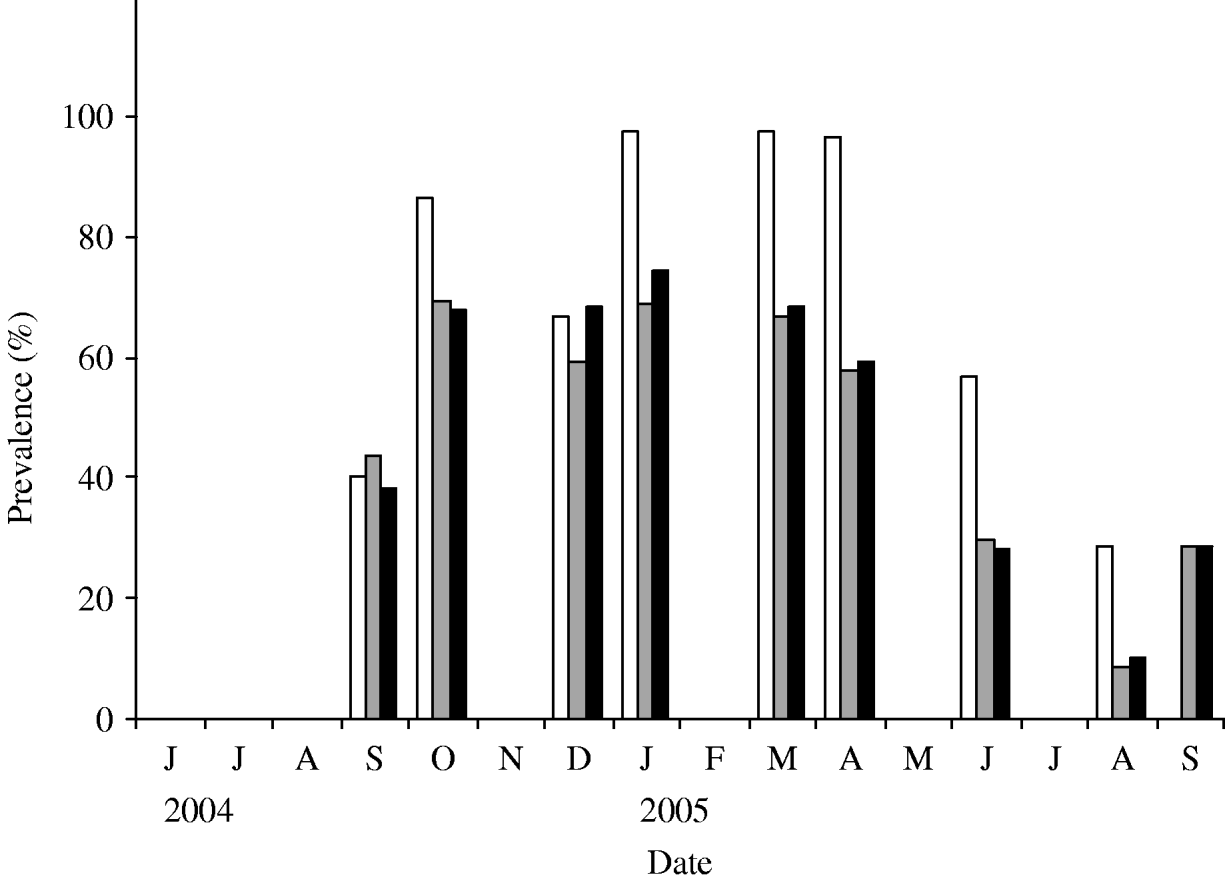
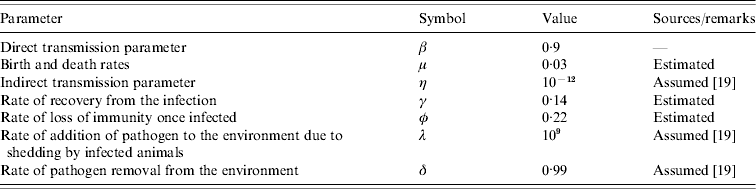
Fig. 2. Prevalence of infection over time. Samples were collected from June 2004 to September 2005. Three prevalence data are shown in this figure: observed prevalence of PCR-positive samples (□), observed faecal culture (![]() ) and corrected faecal culture (■) (see Materials and methods for an explanation).
) and corrected faecal culture (■) (see Materials and methods for an explanation).
The probability that a susceptible animal gets infected depends on the rate of effective contacts with the infected animals. The transmission parameter β(t) was estimated such that the number of new infections at time t+1 is given by the product of the transmission parameter β(t), the number of susceptible animals S(t) and the number of infectious animals I(t) at time t. An animal was considered newly infected if the positive test result was preceded by two consecutive negative test results. In order to estimate the transmission parameter, β, the force of infection for sampling at time t, λ′(t), was estimated as follows:
where I new(t+1) is the number of new infections in the next sampling and D is the sampling interval which gives the duration of exposure. The parameter β is then calculated as
where N′(t) is the total number of animals at time t in the observed data.
The rate of gain in the number of animals in the herd either due to birth or recruitment of new animals, μ, was expected to be equal to the rate of loss of animals due to death or replacement since the total number of animals in the herd remained approximately constant throughout the study. This rate was estimated from the data and was ~0·03 per month, indicating that animals had an adult herd-life expectation of ~3 years. Because of the high value of β and high prevalence, the rate of loss of immunity was estimated as approximately the inverse of the waiting time until a recovered animal gets re-infected and was 0·22 per month. Other parameters such as the indirect contact rates of infection and the survival of the pathogen in the environment are not known and the parameter values were chosen following the assumption of Xiao et al. [Reference Xiao19]. The estimated parameter values are summarized in the Table.
An important concern in epidemiology is whether or not an infectious disease is able to cause an epidemic outbreak. This can be quantified by a single number called the basic reproduction ratio, R 0, which measures the effective transmissibility and provides quantitative criteria for disease control. Effective preventive measures of the possible disease outbreaks would be to reduce the value of R 0. In deterministic models, the disease-free equilibrium is locally asymptotically stable when R 0<1 whereas it is unstable when R 0>1 (see for example [Reference Hethcote29, Reference Hethcote and van den Driessche30]). This means that the disease dies out if R 0<1 and it may maintain itself at an endemic level if R 0>1. R 0 is given by the product of rate of new infections in an entirely susceptible population and the average duration of infectiousness. As discussed in the Appendix, R 0 for the model with n-infectious classes may be obtained by using the next-generation matrix method. The spectral radius of the next-generation matrix, which is the dominant eigenvalue of the same matrix, gives the value of R 0. Solving the characteristic equation, we get:
We see that the basic reproduction ratio R 0 depends on the number of infectious states which translates into the dependence on the distribution of infectious period. In the case of no indirect transmission, η=0 so that
For a single infectious compartment, this reduces to the well-known expression for R 0 as
In order to understand the underlying mechanism of disease transmission, we analysed the model using numerical techniques. The system of differential equations was solved using a fourth-order Runge–Kutta method and the results of disease prevalence and the temporal dynamics were compared with the observed data.
RESULTS
The first faecal sampling of the complete milking herd in March, 2004 indicated that just one (n=102) cow was shedding Salmonella at this time and the isolates from this sample were identified as S. enterica Typhimurium (var. Copenhagen). Six months later, 43·5% of the herd was determined to be infected with Salmonella enterica Cerro (Fig. 2). One animal was shedding S. Kentucky in addition to S. Cerro. In an effort to track the infectious outbreak, the herd was monitored more frequently during the following 12 months. Within 6 weeks the faecal prevalence rate of S. Cerro dramatically increased to 75% and persisted at or near this level for ~6 months. By August, 2005 the number of cows shedding Salmonella had dropped to 9% and the results of a subsequent sampling in September indicated that 29% of the cows were shedding this organism.
Figure 3a shows the observed distribution of infectious periods from the censored data fitted with a gamma distribution. A plot of the survival probability function of the period of infection is presented in Figure 3b. As shown in these figures, persistent shedding of S. Cerro for unusually long duration was observed in the herd. The average period of infection was found to be 1/γ=7·16 months with the variance=2·5. This gives the number infectious stages as n~128.

Fig. 3. (a) Distribution of the duration of infection (infectious period). The solid line is the fitted gamma distribution curve. (b) Survival distribution function for the duration of infection.
Our results on the estimation of β indicated that its value is high at the onset of infection and it decreases rapidly as the infection reaches to the highest. The estimated value of β for each sampling date is plotted in Figure 4. The figure shows a temporal variation of this transmission parameter. Because the whole herd sampling in March 2004 showed no detection of S. Cerro shedding and the data was collected in regular and smaller intervals only after the first detection of high prevalence of salmonella shedding in September 2004, the numbers of new infections prior to September 2004 sampling were not known and it was not possible to accurately estimate β near the beginning of the outbreak. For simplicity, a constant value of β (=0·9) was chosen that best fit the model results with the observed prevalence. It is straightforward to incorporate the time-dependent β in the model if the data is available.

Fig. 4. Variation of the transmission parameter β. The value of β is high at the onset of the outbreak and subsequently decreases to a small but relatively constant value.
Using the estimated parameters, the simulation was run starting at t=0 when a single infectious individual was introduced in an otherwise totally susceptible population. As expected, the prevalence of infection increased initially with the time and starts to subside once it reaches a maximum. In Figure 5, we plot the simulated prevalence of the infection as a function of time and compare it with the observed prevalence in the herd. For comparison of the simulated infection prevalence with the observed one, the origin of the simulation time t=0 has been shifted so that the peak prevalence of the simulated and observed infection approximately match.
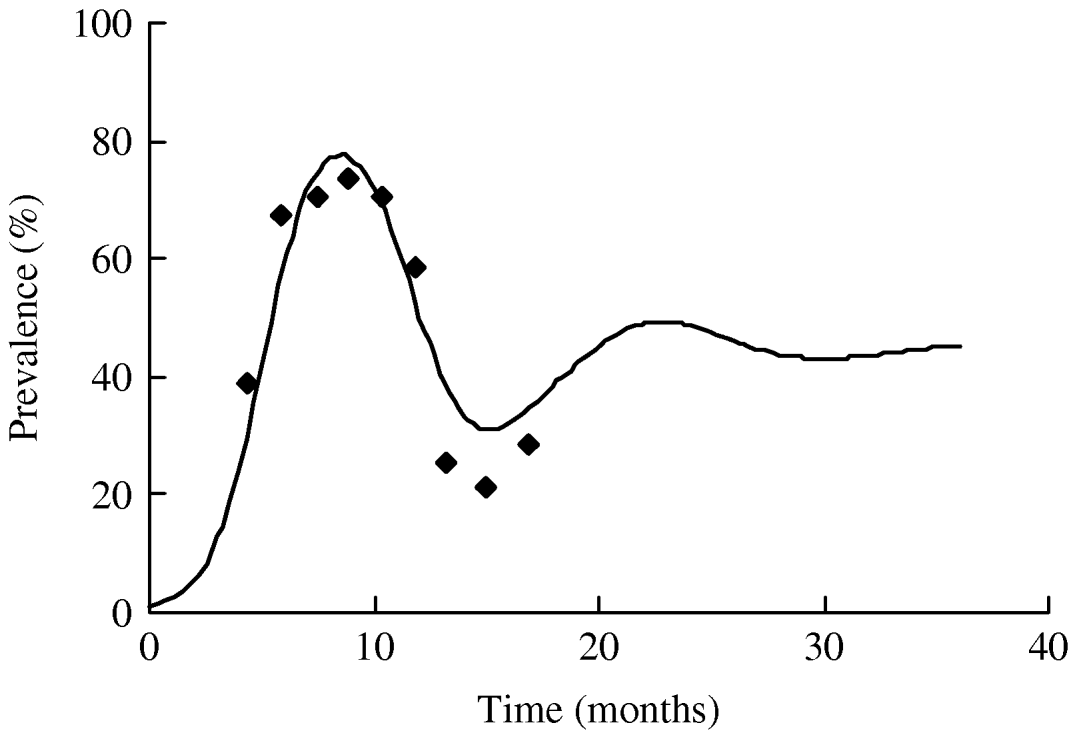
Fig. 5. Observed (◆) and modelled (—) prevalence of S. Cerro in the herd. The data-points reflect the observed prevalence (adjusted) and the continuous line reflects the modelled prevalence with n=100.
The value of R 0 calculated using the average duration of infectiousness and its variance is ~5·8. We plot the dependence of R 0 on the number of infectious stages in Figure 6. It is evident from the figure that with the same average duration of infection, exponential distribution of the infectious periods corresponding to n=1 yields a slightly lower estimate of R 0. As the distribution becomes sharper with the increase in n, the value of R 0 increases as well. R 0 asymptotically reaches a constant for a fixed infectious period corresponding to infinitely many infectious stages (n→∞). However, we note that the distribution of the infectious period has little effect on the value of R 0 since there is only a small variation in the estimates and R 0≫1.
Fig. 6. The relationship between the number of infectious stages (n) and the basic reproduction ratio (R 0).
DISCUSSION
The data that were available for this paper are almost unique. Results of long-term follow-up of a complete milking herd of Salmonella-infected cows has rarely been reported in the literature. In some S. Dublin studies, similar data are available [Reference Wray31], but most of these studies deal with short-term outbreaks often reporting only cross-sectional data [Reference Trueman32, Reference Wedderkopp, Stroger and Lind33]. The herd behaviour of S. Cerro that we observed in this case study indicates that this organism is very well adapted to the dairy cow environment. High rates of new infection were combined with a very long duration of infection. Moreover, there were no obvious signs of clinical disease symptoms associated with the infection in cattle. This was not necessarily due to a lack of observation, since small clinical outbreaks of other salmonella infections (S. Typhimurium and S. Kentucky) were previously noted by the herd owner and veterinarian. The data in the current study indicate that this particular infection can maintain itself relatively well in a dairy herd, potentially leading to long-term infectiousness of dairies with this particular strain.
Of particular interest was our observation of the very long duration of infectiousness. The observed mean duration of ~7 months indicates a very long infectious period per shedder. To be able to model this long infectious period with more accurate distribution, an adopted multi-stage model [Reference Lloyd27] was used. Approximately 100 infectious states were necessary to capture the dynamics of infection.
As with β, other model parameters and rates are likely to have time dependence due to seasonal variation and such seasonal effects may give rise to temporal oscillations in the disease prevalence in the herd. Accurate estimates of the seasonal effects, however, are not readily available and there is a lack of published data in the literature. Here, we aimed at describing the dynamics of the salmonella infection for at least one complete cycle starting from either an infection-free or low prevalence state that matures to a maximum and ultimately the prevalence subsides to a low prevalence. As seen in Figure 5, the model captures the expected dynamics of the S. Cerro infection in the herd. As the actual observed prevalence has an inherent stochastic nature, numbers may not match exactly each month but the qualitative nature of the dynamics is reproduced very well by the model. After the onset of infection, the disease prevalence is high and remains high for a few months. Subsequently, it starts to slide down and hits the lowest observed prevalence in August. The model predicts another smaller peak in the disease prevalence and the height of the second peak may be bigger if we consider time-varying β (decreased to ~0·2 from ~1) so that enough susceptible population is accumulated before hitting a higher force of infection in the next cycle. Continued monitoring of the study herd will permit refinement of the infection dynamics of S. Cerro in subsequent years.
Because of the additional infectious compartments, calculation of R 0 was relatively more complex. The eventual estimate of this parameter was ~5·8, indicating that one infectious individual would on average infect 5·8 susceptible animals. This would generally lead to a massive outbreak of infection in a herd where animals freely mingle. The physical layout of this dairy does allow free and more or less random contact between all animals in the herd and we did indeed observe a large outbreak (see Fig. 2).
Although this study reveals the dynamics of infection in only one dairy herd, the data from recent surveys indicate that S. Cerro is able to cause infections in cattle populations [Reference Mammina15, Reference Wells34]. Although this serotype is a relatively rare cause of disease in humans, cases of human disease associated with S. Cerro have been reported in literature [Reference Bhore, Phadke and Joshi12, Reference Fule and Kaundinya14]. Consequently, prevention or eradication of this infection from cattle herds is desirable. This may not be an easy task, given the high value of R 0 that we estimated from the data. Potential control procedures would include additional environmental hygiene practices (i.e. cleaning waterers and feed alleys), separating animals groups (dry cows vs. milking cows) and introducing effective vaccination practices. There is currently very little field data to make a rational prediction with regard to the impact of these practices on the dynamics of infection. More field research is essential to obtain quantitative estimates on the efficacy of these practices.
ACKNOWLEDGEMENTS
Financial support for this work was provided in part by specific cooperative agreements with the United States Department of Agriculture – Agriculture Research Service (USDA-ARS) and the Food Safety Research and Response Networks through a grant from the USDA-CSREES. We also thank the talented staff of the USDA-ARS Environmental Microbial Safety Laboratory for their technical expertise; and R. Ivanek and R. Mitchell for helpful discussions.
APPENDIX
The expression for R 0 that also includes the indirect transmission may be obtained using next-generation matrix method. The spectral radius of the next-generation matrix, which is the dominant eigenvalue of the same matrix, gives the value of R 0.
From equation (3), we have

For the next-generation matrix, we define the matrices F and V as
where F i(x) is the number of new infections in the ith compartment from xj infectious individuals and Vi (x) is the net change of animals in the ith compartment by any other means. The rates are evaluated at the disease-free equilibrium x=x 0. For the model, these matrices are given as follows:

The characteristic equation for the next-generation matrix FV −1 is given by

Solving for the dominant eigenvalue, we get

The R 0 for the model with n-infectious stages and no indirect transmission may be given by the sum of the contributions from each individual stage

Alternatively, the same expression may be derived from the integral method. Following Lloyd [Reference Lloyd26], R 0 is given by
For gamma-distributed infectious periods, we replace the value of f(τ) from equation (2)

For the single infectious compartment without indirect transmission, the usual expression for R 0 is retained
DECLARATION OF INTEREST
None.











